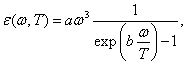1.1 Záření dokonale černého tělesa
Ve skutečnosti se jedná o idealizovaný model, v přírodě se dokonale černá tělesa nevyskytují. Mnohé tepelné zářiče se však svými vlastnostmi tomuto modelu velmi blíží (např. Slunce a ostatní hvězdy, nebo dokonce i vlákno žárovky). V pozemských podmínkách bývá dokonale černé těleso reprezentováno dutinovým zářičem.
Tepelné záření v dutině,
které je v termodynamické rovnováze s jejími stěnami o teplotě T, je obvykle popisováno spektrální hustotou energie e(w,T). Teoretická
formulace závislosti spektrální hustoty energie na frekvenci (vlnové délce)
byla velkou výzvou pro fyziky konce 19. století. Popisuje ji několik empirických zákonů.
Prvním z nich je Rayleighův-Jeansův zákon. Lze jej odvodit v rámci klasické teorie, platí však pouze v oblasti nízkých frekvencí a osudově selhává
pro frekvence vysoké.
Další empirický zákon, Wienův,
popisuje vyzařování dokonale černého tělesa v oblasti vysokých frekvencí,
selhává ale naopak pro frekvence nízké.
Teprve zákon Planckův přinesl úplný popis záření dokonale černého tělesa. V rámci klasické fyziky jej však není možno odvodit. Pro jeho teoretické zdůvodnění musel Max Planck postulovat svou proslulou kvantovou hypotézu. Problém záření dokonale černého tělesa tak stál u samotného zrodu kvantové fyziky.
Vybrané vzorce a vztahy
Označme 
objemovou hustotu energie tepelného záření o teplotě T nesenou monochromatickými složkami o úhlových
frekvencích z intervalu 
pak pod spektrální
hustotou energie tohoto záření rozumíme
kde 
je Boltzmannova konstanta.
kde a a b jsou konstanty určované pomocí
experimentálních dat.
kde a a b jsou
konstanty určované pomocí experimentálních dat.
Literatura
[1] PLANCK, M. Verhandlungen der Deutschen physikalischen
Gesellschaft, 1900, Bd. 2.
[2] HAJKO, V., aj. Fyzika v experimentoch. 1. vyd. Bratislava: Veda, 1988. 415 s. s. 55-61.
