1.2 Klasická teorie záření dokonale černého tělesa
Elektromagnetické pole (záření)
uzavřené v dutině konečného objemu V je možno chápat jako soustavu
nezávislých lineárních harmonických oscilátorů.
Například pro dutinu ve tvaru kvádru lze Maxwellovy rovnice převést pomocí Fourierových řad na nekonečnou soustavu
nezávislých obyčejných diferenciálních rovnic, které svým tvarem odpovídají
pohybovým rovnicím pro netlumené lineární harmonické oscilátory. Tyto
oscilátory mají obecně různé charakteristické úhlové frekvence (záření dokonale černého tělesa není monochromatické) a jednoduchým výpočtem je možno
určit, kolika z nich přísluší úhlové frekvence ze zadaného intervalu (w,w+Dw) [1]:
Z klasické statistické fyziky
je známo, že střední energie e(T) lineárního harmonického oscilátoru, který je
v kontaktu s termostatem o teplotě
T, je dána vztahem (viz též ekvipartiční
teorém)
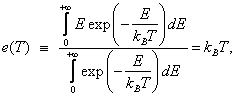
kde kB je Boltzmannova
konstanta. Pro energii
oscilátorů reprezentujících elektromagnetické pole v dutině, jejichž
frekvence jsou z intervalu (w,w+Dw), můžeme tedy psát
a pro spektrální hustotu energie
Poslední uvedený vztah nese na
paměť anglických fyziků, kteří jej odvodili, název Rayleighův-Jeansův zákon.
Tento zákon však souhlasí
s experimentálními daty jen pro malé hodnoty úhlových frekvencí (a tedy
jen pro dlouhé vlnové délky). V oblasti vysokých frekvencí zcela selhává.
Kromě toho celková objemová hustota energie elektromagnetického záření v
dutině, 
, je podle
Rayleighova-Jeansova zákona nekonečná. Osudové selhání klasické teorie
v oblasti vysokých frekvencí bylo příznačně nazváno ultrafialovou katastrofou.
Literatura
[1] BEISER, A. Úvod do moderní fyziky. 1. vyd. Praha: Academia, 1978. 628 s. s. 389-392.
