![]() 6.5.1 Vibrace molekul
6.5.1 Vibrace molekul
Harmonické přiblížení
Rozklad na nezávislé harmonické oscilátory
Vibrace dvouatomové molekuly
Vibrace trojatomové lineární symetrické molekuly
| Symetrický vazebný vibrační mód | |
| Asymetrický vazebný vibrační mód | |
| Deformační vibrační mód (dvojnásobně degenerován, obdobná deformace může probíhat v rovině kolmé k nákresně) |
Podle kvantové teorie (viz např. lineární harmonický oscilátor) musí částice i v základním stavu (nejnižším dovoleném energetickém stavu) kmitat s nenulovou kinetickou energií (energie nulových kmitů). U harmonického oscilátoru je střední výchylka částice z rovnovážné polohy nulová pro všechny energetické stavy. U oscilátoru anharmonického, jsou odchylky z rovnovážných poloh malé jen pro nejnižší energetické stavy. Přibližná představa o zaujmutí rovnovážných poloh atomy je tedy přijatelná.
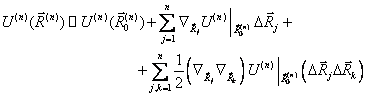
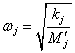 .
.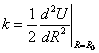 . Zde M představuje hmotnost atomu
a R0 je délka vazby odpovídající
rovnovážné poloze –
. Zde M představuje hmotnost atomu
a R0 je délka vazby odpovídající
rovnovážné poloze – 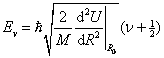 ,
,