6.5 Spektra molekul
Při řešení molekul (ale
též jiných systémů, např. pevných látek) se většinou vychází z Bornovy-Oppenheimerovy
aproximace, resp. adiabatické aproximace, která
umožňuje rozdělit řešení kvantového problému pro jádra a elektrony na řešení
dvou pohybových rovnic: Schrodingerovu rovnici elektronového systému v poli
nehybných jader či obecněji iontových zbytků a pohybovou
rovnici těchto iontových zbytků, v níž jako dodatečný potenciál
vystupuje energie elektronového systému.
Pokud tedy chceme určit
energetické spektrum molekuly, bývá prvotní spočtení jejího elektronového spektra, tj. určení
dovolených hodnot energie elektronů Ee.
V případě izolovaného atomu se vliv pohybu jádra v těžišťové soustavě
může započítat metodou
redukované hmotnosti. U molekuly ovšem mohou jednotlivé
iontové zbytky vykonávat v těžišťové soustavě jednak rotační pohyb (rotace molekuly jako
celku), jednak vibrační pohyby (vibrace molekuly, kdy se jednotlivé iontové
zbytky pohybují vůči sobě navzájem).
Celková energie molekuly E je součtem energie elektronového systému 
, vibrační energie molekuly 
a rotační energie molekuly 
, tedy
.
Výsledné spektrum je
kombinací elektronového, rotačního a vibračního spektra. Pro vzdálenosti dvou
sousedních čar elektronového, vibračního a rotačního spektra platí přibližně
.
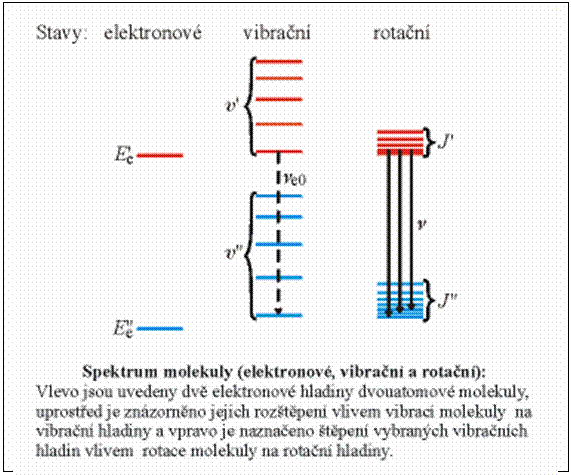
Původní degenerované
elektronové energetické hladiny se v případě vibrací rozpadají na blízké
vibrační hladiny, pokud navíc molekula rotuje, rozpadne se dále každá
z vibračních hladin na velmi blízké rotační hladiny, které tvoří
kvazispojité pásy rotačně-vibračního spektra. Emisní či absorpční spektrum
molekuly je v tomto případě pásové.
Rotačně-vibrační elektromagnetická spektra se pozorují v infračervené oblasti. Pokud dochází pouze ke změně rotačního stavu pozorujeme rotační, spektrum ve vzdálené infračervené a mikrovlnné oblasti.
