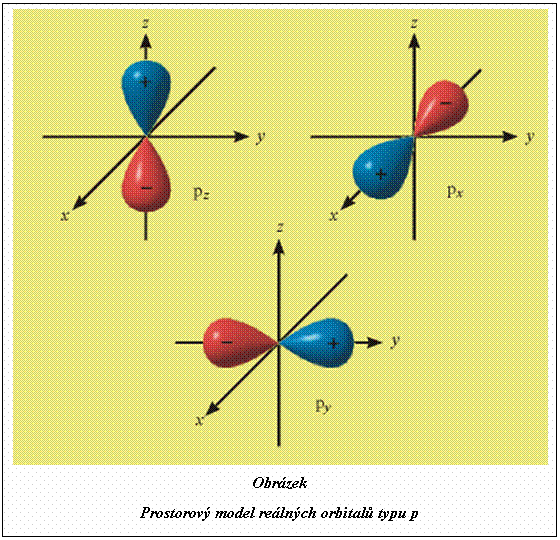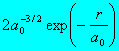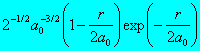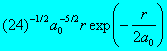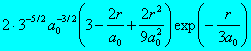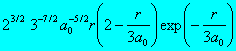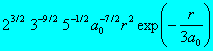2.1 Znázornění atomových orbitalů

Atomové orbitaly je možno znázornit různými způsoby.

Radiální část vlnové funkce pro několik prvních hodnot kvantových čísel n a l je uvedena v tabulce:

n	l	Rnl(r)
1	0
2	0
2	1
3	0
3	1
3	2

Konstanta je Bohrův poloměr atomu.

Protože radiální část vlnové funkce závisí pouze na r, je možné zobrazit její průběh pomocí grafu ve dvou osách. Buď se zobrazuje přímo funkce , nebo její druhá mocnina, tj. , popřípadě hodnota , jelikož výraz představuje pravděpodobnost nalezení elektronu ve vzdálenosti r až od jádra bez ohledu na směr. Jinak řečeno, jde o pravděpodobnost nalezení elektronu v kulové vrstvě o poloměru r a tloušťce dr.

Angulární část vlnové funkce představují tzv. kulové funkce (též sférické funkce), jejichž tvar pro několik prvních hodnot l a m je uveden v tabulce:

L	m	Ynl(q, j )
0	0
1	0
1	±1
2	0
2	±1
2	±2

Kulové funkce jsou funkcemi dvou úhlů, navíc se jedná o komplexní funkce, proto je jejich znázornění obtížnější než v případě radiální vlnové funkce. Z tohoto důvodu se znázorňuje většinou veličina , která už je reálnou funkcí a navíc závisí jen na úhlu . Výraz má význam pravděpodobnosti nalezení elektronu ve směrech určených úhly mezi  a a mezi   a. Jinak řečeno, jde o pravděpodobnost nalezení elektronu v elementu prostorového úhlu . Funkci |Y_nl|² je možno znázornit ve formě polárního diagramu, tj. ve směru daném úhly a se vykreslují body ve vzdálenosti od počátku. Graf tedy představuje plochu v prostoru. Vzhledem k tomu, že závisí pouze na úhlu , je tato plocha symetrická podle osy z. Pro získání představy o tvaru funkce stačí znázornit řez s libovolnou rovinou procházející osou z, např. rovinnou xz ().

Znázornění celých atomových orbitalů (AO) je podstatně těžší než zobrazení samostatné radiální části AO nebo angulární části AO. Jedná se o komplexní funkce tří proměnných r, q a j. Abychom nemuseli zobrazovat reálnou a imaginární část AO , volí se pro zobrazení

a) hustota pravděpodobnosti nalezení elektronu v bodě , tedy veličina ,

b) reálné atomové orbitaly , které se získají vhodnou lineární kombinací původních (komplexních) atomových orbitalů s pevnou hodnotou n a l , ale různou hodnotou m,

c) hustota pravděpodobnosti nalezení elektronu v bodě pro stavy odpovídající reálným atomovým orbitalům z bodu b), (viz též následující kapitolu).

V případě b se využívá skutečnosti, že libovolná lineární kombinace řešení bezčasové Schrödingerovy rovnice je rovněž jejím řešením. Reálné orbitaly pro dané n a l už ovšem nejsou na rozdíl od původních funkcí vlastními funkcemi operátoru z-ové komponenty orbitálního momentu hybnosti . Obecně tedy nepopisují stavy s určitou hodnotu . Např. reálné AO typu p dostaneme kombinacemi:

,

,

.

---

---