5.8 Taylorův rozvoj (funkcí více reálných proměnných)

Věta (Taylorova)

Nechť má funkce  f  má na nějakém okolí bodu  a  spojité všechny parciální derivace až do řádu  m. Pak platí[1]

.

Poznámka

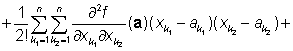
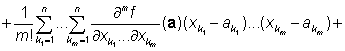
Podle této věty je možno nahradit na nějakém malém okolí bodu  a  obecnou funkci  f  jednodušším polynomem více proměnných. Tento polynom nazýváme Taylorovým polynomem stupně  m  funkce  f  v bodě  a.  Používáme pro něj symbolické označení T_m(x;f,a).  Chyby, kterých se při této přibližné náhradě dopustíme, jsou řádu m+1,  tj. jsou úměrné  .  Hovoříme tedy o přiblížení m-tého řádu.

Poznámka

Všimněte, že pro m = 1 přechází Taylorova věta na větu o totálním diferenciálu. Taylorova věta je tedy zobecněním věty o totálním diferenciálu.

Poznámka

Pečlivě porovnejte obsah této kapitoly s kapitolou věnovanou Taylorovu rozvoji funkcí jedné reálné proměnné.

[1] Pod symbolem o(xⁿ) rozumíme libovolnou funkci, která splňuje .