5.4 Parciální derivace

Definice (první parciální derivace)

Nechť je funkce f(x) definována na nějakém okolí bodu  a.  První parciální derivací (často však stručněji parciální derivací) funkce  f   podle proměnné  x_k  v bodě  a  nazveme

.

Užíváme pro ni zpravidla označení  .

Poznámka

Výpočet parciální derivace podle proměnné    v bodě  a  odpovídá výpočtu obyčejné derivace (viz zde) nové funkce jedné reálné proměnné . Kromě zvolené proměnné považujeme tedy během výpočtu všechny zbývající proměnné za konstanty.

Věta (algebra derivací)

Pokud mají pravé strany rovností smysl, platí [1]

,

,

,

,

.

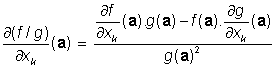Poznámka (vyšší parciální derivace)

Opakovaným parciálním derivováním, pokud je to možné, získáme vyšší parciální derivace zadané funkce více reálných proměnných [2].

Opakované derivování můžeme provést podle stejné nezávislé proměnné. Získáme tak druhou, třetí atd. parciální derivaci funkce  f  podle této proměnné. Používáme označení

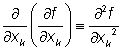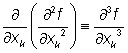,  atd.

Pokud opakované derivování provádíme podle různých proměnných, dostáváme tzv. smíšené vyšší derivace zadané funkce. Pro smíšenou vyšší derivaci pak používáme označení

.

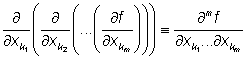Index m u symbolu parciálního derivování v čitateli označuje řád parciální derivace.

Věta

Nechť má funkce  f  v bodě  a  spojité obě smíšené druhé derivace    i  . Pak jsou si tyto derivace rovny.

Poznámka

Pro „rozumné“ funkce nezáleží tedy ve smíšených derivacích na pořadí derivování.

[1] Porovnejte s analogickou větou pro funkce jedné reálné proměnné.

[2] Porovnejte s definicí vyšších derivací reálné funkce jedné reálné proměnné.