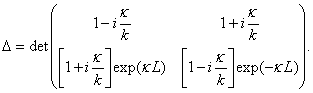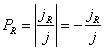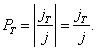4.9.17 Jednorozměrná pravoúhlá potenciálová bariéra
Potenciál
Jednorozměrná pravoúhlá potenciálová bariéra odpovídá modelovému potenciálu
kde 
je kladná konstanta.
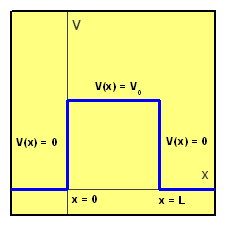
Typický průběh pravoúhlé potenciálové bariéry je znázorněn na obrázku.
Řešená úloha
Pro částici s danou energií
E hledáme pravděpodobnosti průniku výše zadanou
bariérou a odrazu od ní. Jak je popsáno na jiném místě, měření těchto
pravděpodobností můžeme uspořádat následujícím způsobem: Bariéru ozařujeme
zleva ustáleným proudem částic, jemuž odpovídající hustotu toku
označíme symbolem j. Některé z částic, které
dopadnou na bariéru, se od ní odrazí, jiné bariérou projdou. Odraženým částicím
odpovídá jistá stacionární hustota toku, kterou označíme 
Částicím prošlým
bariérou pak přiřadíme hustotu toku 
Z orientace směrů
pohybu dopadajících, odražených a prošlých částic plyne: 
a 
Pravděpodobnosti odrazu a průchodu bariérou pak můžeme určit ze vztahů
a 
Podle definice
počítáme totiž například pravděpodobnost odrazu
jako 
Vzhledem ke
stacionárnímu uspořádání dopadne na bariéru za čas t celkem 
částic a za stejný
čas se od bariéry odrazí 
částic. Limitní
přechod 
odpovídá zřejmě
přechodu 
Proto můžeme psát
Podobné úvahy můžeme provést, a získat tak odpovídající
vztah, i pro pravděpodobnost průchodu 
Výše popsaný experiment má stacionární uspořádání a navíc
požadujeme, aby částice dopadající na bariéru měly zadanou energii. Hlubší
analýza, která však zcela překračuje rámec našeho výkladu, ukazuje, že hustoty toků pravděpodobnosti
odpovídající stacionárním vlnovým funkcím je možno ztotožnit s výše zavedenými
hustotami toků částic. Přímo se proto nabízí možnost hledat
pravděpodobnosti a 
pomocí stacionární Schrödingerovy rovnice.
Odraz od pravoúhlé potenciálové bariéry - řešení pomocí stacionární
Schrödingerovy rovnice
Jako ilustraci toho, jak se stacionární Schrödingerova
rovnice používá při nalezení pravděpodobností průchodu a odrazu částic od
pravoúhlé potenciálové bariéry, si uveďme výsledky plynoucí pro částice,
jejichž energie E je menší než výška
bariéry 
Podrobné řešení pro částici o hmotnosti M nacházející se v poli výše uvedeného
potenciálu je možno nalézt zde.
Z něj vyplývá, že stacionární vlnové funkce nabývají pro zadanou energii 
tvaru
pro 
pro 
pro 
kde 
a 
Vlnovým funkcím tohoto tvaru odpovídají hustoty toků pravděpodobnosti
pro
pro 
Vlevo od bariéry je hustota toku dána součtem příspěvků odpovídajících dopadajícím a odraženým částicím:
a 
Vpravo od bariéry se mohou podle zadání nacházet pouze částice
prošlé. Jim zřejmě odpovídá tok 
V této oblasti se
naopak nemohou nacházet žádné částice pohybující se v opačném směru. Proto
musíme položit
Pro pravděpodobnosti průchodu částice pravoúhlou bariérou a odrazu od ní takto získáme
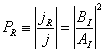a 
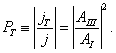
Konstanty 
a 
nejsou ovšem navzájem
nezávislé. Z podrobné analýzy
vyplývá, že např. konstanty a jsou násobky
konstanty kde příslušné
multiplikativní faktory závisejí pouze na energii E a parametrech zadávajících potenciálovou
bariéru. Konečné formule pro pravděpodobnosti odrazu a průchodu částice
studovanou bariérou můžeme takto psát ve tvaru
a 
kde
