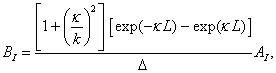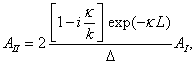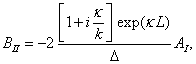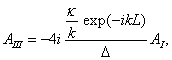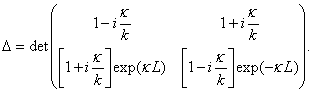4.9.18 Jednorozměrná pravoúhlá potenciálová bariéra - podrobné řešení stacionární Schrödingerovy rovnice

Stacionární Schrödingerovu rovnici řešíme pro jednorozměrnou pravoúhlou potenciálovou bariéru odděleně na intervalu (0,L) a mimo něj. Jednotlivé části vlnové funkce zúžené na odpovídající intervaly osy x označme (pozn. 1)

pro

pro

pro

Pro potenciál s nespojitostmi typu konečného skoku v bodech x = 0 a x = L musí být vlnová funkce y v uvedených bodech spojitá a mít v nich spojité první derivace (pozn. 2). To znamená, že je nutno splnit tzv. sešívací podmínky

Řešení stacionární Schrödingerovy rovnice

Stacionární Schrödingerova rovnice nabývá po výše naznačeném rozdělení vlnové funkce y na tři části a po jednoduchých úpravách tvaru

.

Řešení nově získaných rovnic můžeme hledat obvyklým způsobem (pozn. 3). V následujícím výkladu se soustředíme jen na speciální případ pro bychom postupovali stejně.

Pro energie z intervalu můžeme výše uvedené rovnice přepsat do tvaru

kde a Jejich obecné řešení je dáno formulemi

Zatím neznámé konstanty A a B určíme pomocí sešívacích podmínek a dalších speciálních požadavků na vlnovou funkci y.

Především, ze všech řešení jsou přijatelná jen ta, která odpovídají (podle zadání problému) proudu částic bombardujících studovanou bariéru zleva. Vpravo od bariéry se proto mohou částice pohybovat pouze od bariéry pryč, tedy v kladném směru osy x. Jak je ukázáno na jiném místě, je tato podmínka splněna, je-li

Dále, sešívací podmínky poskytují čtyři homogenní lineární algebraické rovnice pro zbývajících pět neznámých integračních konstant:

Čtyři z těchto konstant můžeme proto vyjádřit pomocí jedné vybrané. Mají-li být tedy sešívací podmínky splněny, můžeme například psát

kde

(1)

Symboly a zde označujeme polouzavřené intervaly, tedy množiny všech reálných x splňujících resp. Podobně symbolem resp. označujeme interval uzavřený resp. otevřený, tj. množiny všech reálných x splňujících resp.

(2)

Ze Schrödingerovy rovnice zapsané ve tvaru vyplývá, že pro potenciál s nespojitostmi typu konečného skoku bude mít stejné nespojitosti i druhá derivace vlnové funkce y. Z diferenciálního počtu ale víme, že v takovém případě bude funkce sama i její první derivace spojitá.

(3)

Uvedené rovnice jsou lineární obyčejné diferenciální rovnice s konstantními koeficienty a nulovou pravou stranou. O způsobu jejich řešení se může čtenář poučit např. v REKTORYS, K., aj. Přehled užité matematiky. 4. vyd. Praha: SNTL, 1981. 1139 s. s. 649-652.

---

---