3.4.1 Izotermický děj

Izotermický děj

Předpokládáme, že termodynamická teplota T plynu v soustavě je v celém průběhu děje stálá. Volně se mění objem V a tlak p. Nemění se tedy vnitřní energie soustavy. Veškeré přijaté teplo se mění v práci vykonanou soustavou na okolí. Na začátku i konci děje je shodná teplota. Stavová rovnice ideálního plynu má pro počáteční stav plynu tvar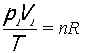

3.4.1. image1.bmp (15318 bytes)

a pro koncový stav

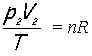
 3.4.1. image2.bmp (15510 bytes)

Porovnáním obou vztahů obdržíme další vztah, který se označuje jako Boylův-Mariottův zákon:

p1V1 = p2V2, nebo pV = konst.

Boylův - Mariottův zákon. Je-li teplota ideálního plynu stálá, pak součin tlaku a objemu plynu je konstantní. Takovýto děj nazýváme izotermický.

 

Závislost tlaku na objemu se dá vyjádřit i graficky. Z matematického vyjádření Boyleova-Mariottova zákona je zřejmé, že křivka bude mít tvar hyperboly. Přesněji její jedné větve. Nazýváme ji izotermou.

 1.2 video.jpg (1686 bytes)

Při izotermickém ději se nemění vnitřní energie termodynamické soustavy. Veškeré teplo přijaté soustavou se mění v práci Q = W. Práce při izotermickém ději je maximální vzhledem k přijatému teplu. Z prvního termodynamického principu můžeme rovněž odvodit vztah pro práci:

Izotermická expanze. Izotermické rozpínání ideálního plynu sledujeme pokud plyn koná práci proti vnějším silám a přijímá ekvivalentní teplo z okolí.

V2 >V1 => W > 0

Izotermická komprese. Izotermické stlačování ideálního plynu probíhá, když na plynu je konána práce a plyn odevzdává ekvivalentní teplo okolí.

V2 < V1 => W < 0

 

 

Up 3.4.1 Izotermický děj 3.4.2 Izobarický děj 3.4.3 Izochorický děj 3.4.4 Adiabatický děj 3.4.5 Polytropický děj