2.5 Lokální extrémy
Teorii naleznete v kapitole 5.9 a 5.9.2 Multimediální encyklopedie nebo v kapitole 2.5 Breviáře.
Příklad 1
Nalezněte lokální extrémy funkce f(x,y) = xy ![]() +
+ ![]()
Řešení
Body, v nichž jediných můžeme extrémy očekávat, hledáme jako nulové body parciálních derivací. ![]() f(x,y)
f(x,y)
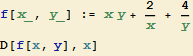
![]()
![]() f(x,y)
f(x,y)
![]()
![]()
Nalezneme bod, ve kterém jsou obě první derivace nulové.
![]()
![]()
Funkce má nulové obě první derivace v bodě (1, 2).(Pozn. Ostatní nalezené body nemají reálné souřadnice.)
Zda se extrém v bodě (1, 2) opravdu vyskytuje a pokud ano, tak jakého typu, o tom rozhodneme pomocí druhých parciálních derivací.
Sestavíme Hessovu matici v bodě (1, 2).
A = 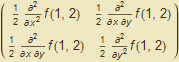
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Můžeme tedy psát:
A = ![]()
Vypočteme vlasní čísla Hessovy matice:
![]()
![]()
![]()
![]()
![]()
![]()
Obě vlastní čísla jsou tedy kladná, Hessova matice je tedy pozitivně definitní a funkce f(x,y) = xy ![]() +
+ ![]() nabývá v bodě (1, 2) lokálního minima.
nabývá v bodě (1, 2) lokálního minima.
Na závěr můžeme znázornit graf zadané funkce na okolí bodu (1, 2). Z grafu funkce vidímě, že funkce f(x,y) = xy ![]() +
+ ![]() skutečně nabývá minima v bodě (1, 2).
skutečně nabývá minima v bodě (1, 2).
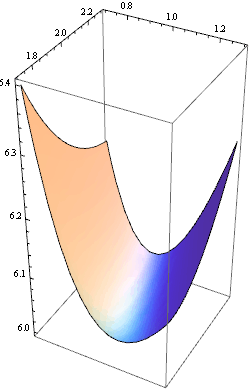
Příklad 2
Nalezněte lokální extrémy funkce f(x,y) = ![]() - 3xy
- 3xy
Řešení
Body, v nichž jediných můžeme extrémy očekávat, hledáme jako nulové body parciálních derivací. ![]() f(x,y)
f(x,y)
![]()
![]()
![]() f(x,y)
f(x,y)
![]()
![]()
Nalezneme bod, ve kterém jsou obě první derivace nulové.
![]()
![]()
Funkce má nulové obě první derivace ve dvou bodech: (1, 1) a (0,0). (Ostatní body, které nalezla Mathematica, nemají reálné souřadnice.)
Nyní pomocí druhých derivací prověříme, zda se v těchto bodech vyskytují lokální extrémy a pokud ano, tak určíme jejich typ.
a) bod (1, 1)
Sestavíme Hessovu matici v bodě (1,1).
A = 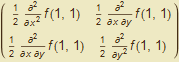
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Můžeme tedy psát:
A = 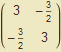
Vypočteme vlasní čísla Hessovy matice:
![]()
![]()
Obě vlastní čísla jsou tedy kladná, Hessova matice je tedy pozitivně definitní a funkce f(x,y) = ![]() - 3xy nabývá v bodě (1,1)) lokálního minima.
- 3xy nabývá v bodě (1,1)) lokálního minima.
Na závěr můžeme znázornit graf zadané funkce na okolí bodu (1,1). Z grafu funkce vidímě, že funkce f(x,y) = ![]() - 3xy skutečně nabývá minima v bodě (1, 1).
- 3xy skutečně nabývá minima v bodě (1, 1).
![]()
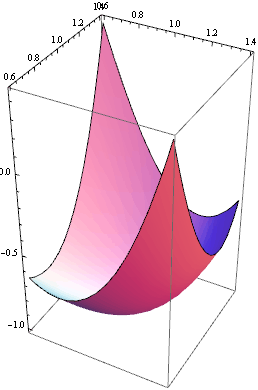
b) bod (0, 0)
Sestavíme Hessovu matici v bodě (1,1).
A = 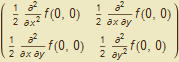
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Můžeme tedy psát:
A = 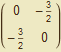
Vypočteme vlasní čísla Hessovy matice:
![]()
![]()
Vlastní čísla mají různá znaménka, Hessova matice je tedy indefinitní a funkce f(x,y) = ![]() - 3xy má v bodě (0,0) sedlový bod.
- 3xy má v bodě (0,0) sedlový bod.
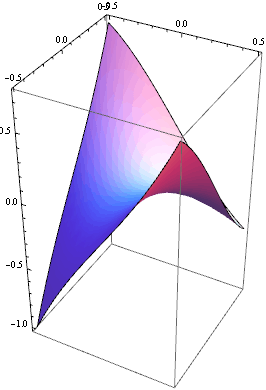
U funkce dvou proměnných lze sedlový bod graficky znázornit. Zobrazíme si graf zadané funkce na okolí sedlového bodu.
![]()
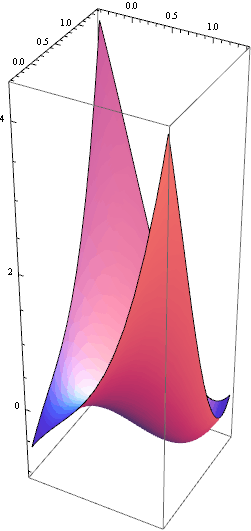
Na závěr si znázorníme graf funkce f(x,y) = ![]() - 3xy na oblasti obsahující oba stacionární body, tzn. lokální minimum v bodě (1,1) i sedlový bod v bodě (0,0).
- 3xy na oblasti obsahující oba stacionární body, tzn. lokální minimum v bodě (1,1) i sedlový bod v bodě (0,0).
![]()
Příklad 3
Nalezněte lokální extrémy funkce f(x,y,z) = ![]()
Řešení
Postup je stejný jako v předcházejících případech. Nejdříve hledáme nulové body prvních parciálních derivací.
![]()
![]()
![]()
![]()
![]()
![]()
Nyní nalezneme body, pro které jsou všechny první derivace rovny nule.
![]()
![]()
Existuje tedy jediný bod (1,0,1), v němž může zadaná funkce lokálního extrému nabývat.
Ověření, zda je tento bod skutečně bodem lokálního extrému, provedeme pomocí druhých derivací, přesněji podle znamének vlastních čísel matice
A = 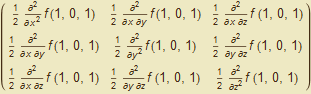
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
MAtice A má tedy v bodě (1, 0, 1) tvar
A = 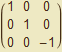
Vlastní čísla diagonální matice jsou rovny číslům na hlavní diagonále. Můžeme je přesto vypočítat programem Mathematica.
![]()
![]()
Vlastní čísla matice A mají různá znaménka, v bodě (1, 0, 1) tedy není lokální extrém, ale jen sedlový bod.
Graf funkce tří proměnných se znázornit nedá, jedná se o trojrozměrnou "plochu" ve čtyřrozměrném prostoru. Můžeme se ale pokusit znázornit např. tři řezy grafem této funkce procházejícími sedlovým bodem na okolí tohoto sedlového bodu, např. rovinami x=1, y=0 a z=1.
Řez grafu rovinou x=1 procházející sedlovým bodem:
![]()
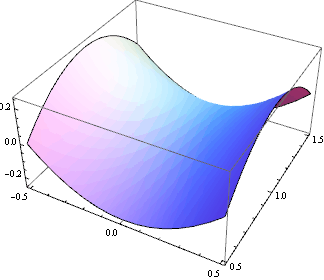
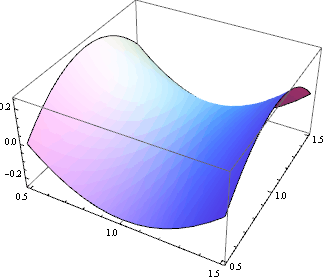
Řez grafu rovinou y=0 procházející sedlovým bodem:
![]()
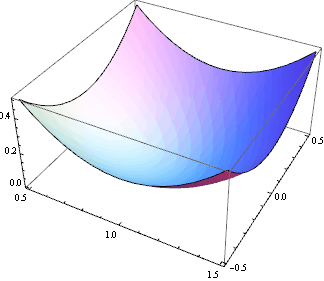
Řez grafu rovinou z=1 procházející sedlovým bodem:
![]()
U funkce tří proměnných jsou naše geometrické představy o grafu funkce již značně limitovány. Přesto z řezů grafu rovinami x=1 a y=0 je vidět, že se v bodě (1,0,1) opravdu nachází sedlový bod.