4.4.2 Věty o derivacích

spojitost diferencovatelné funkce
algebra derivací
derivace inverzní funkce
derivace složené funkce

Věta (spojitost diferencovatelné funkce)

Funkce diferencovatelná v zadaném bodě je v tomto bodě spojitá. Funkce diferencovatelná na nějakém otevřeném intervalu je spojitá na tomto intervalu.

Věta (algebra derivací)
Pokud mají pravé strany rovností smysl, platí (o algebraických operacích s funkcemi viz zde)

,

,

,

,

.

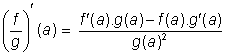Věta (derivace inverzní funkce)

Nechť má funkce  f  funkci inverzní a v bodě  a  existuje její první derivace  , která je nenulová.  Pak existuje první derivace funkce  v bodě     a platí

.

Poznámka

Větu o derivování inverzní funkce (tentokrát v obecném bodě  x)  můžeme zapsat i ve tvaru

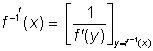
a číst: Inverzní funkci derivuj tak, že derivuješ funkci, k níž je tato funkce inverzní, podle její nezávislé proměnné (zde ji značíme  y),  z výsledku udělej reciprokou hodnotu a za proměnnou  y  nakonec dosaď .

Věta (derivace složené funkce)

Nechť funkce  g  a  f  mají první derivace    a  ,  kde  .  Pak existuje i derivace složené funkce    a platí

.

Poznámka

Větu o derivování složené funkce (v obecném bodě  x)  můžeme zapsat i ve tvaru

a číst: Složenou funkci derivuj tak, že nejdříve derivuješ vnější funkci podle její nezávislé proměnné (zde ji značíme  y) a za proměnnou  y dosadíš  ,  a pak  vše vynásob derivací vnitřní funkce podle její nezávislé proměnné (x).