2

2. POHYBY TÌLES V HOMOGENNÍM TÍHOVÉM POLI ZEMÌ

Za pohyby tìles v homogenním tíhovém poli Zemì považujeme ty pohyby, jejichž trajektorie jsou vzhledem k rozmìrùm Zemì nesrovnatelnì malé. Pøedpokládáme, že na pohybující se tìlesa pùsobí pouze tíhová síla , která ji udìluje tíhové zrychlení .

2.1.VOLNÝ PÁD

Volný pád je zvláštní pøípad rovnomìrnì zrychleného pohybu s nulovou poèáteèní rychlostí.

Animovaný prùbìh volného pádu

Tento pohyb koná tìleso volnì puštìné v blízkosti povrchu Zemì ve vakuu. Trajektorií volného pádu je èást svislé pøímky.

Zrychlení volného pádu se nazývá tíhové zrychlení . Vektor tíhového zrychlení urèuje v daném místì zemského povrchu svislý smìr. Velikost tohoto zrychlení závisí na zemìpisné poloze a výšce místa nad povrchem Zemì. V naší zemìpisné šíøce v blízkosti povrchu Zemì je velikost tíhového zrychlení , avšak pøi øešení úloh vìtšinou používáme zaokrouhlenou hodnotu g = 10 m.s^-2. Velikost normálního tíhového zrychlení , která byla stanovena dohodou, je

g_n= 9,80665 m.s^-2.

Pokusy s volným pádem provádìl již Galileo Galilei. ( 1564 - 1642 ), který také prokázal, že volný pád je rovnomìrnì zrychlený pohyb.

Okamžitá rychlost a dráha s volnì padajícího tìlesa je urèena vztahem

kde je tíhové zrychlení a t doba trvání volného pádu. Z tìchto vztahù lze urèit dobu pádu , pøípadnì také velikost rychlosti pøi dopadu tìlesa .

Mechanická energie pøi volném pádu tìlesa

Nacházíme se v izolovaném systému, kde platí zákon zachování mechanické energie, tedy kde souèet energie kinetické a potenciální je stálý. Úbytek jedné z energií se projeví pøírùstkem energie druhé.

Na poèátku volného pádu držíme tìleso v nìjaké výšce nad povrchem Zemì. V tomto okamžiku je celková energie tìlesa rovna jeho potenciální energii a jeho kinetická energie je nulová, nebo je dosud v klidu. Od okamžiku, kdy tìleso pustíme, a kdy se zaèíná pohybovat ve svislém smìru, postupnì roste jeho kinetická energie a klesá jeho potenciální energie. V okamžiku dopadu tìlesa na zem je celková energie rovna kinetické energii tìlesa a potenciální energie tìlesa je nulová.

Poznámka: Pøedstava o platnosti konstantního souètu kinetické a potenciální energie je pouze pøibližná. Ve skuteènosti bychom nemìli opomenout odpor vzduchu a tedy i energii pøemìnìnou pøi pøekonávání tohoto odporu.

NEWTONOVA TRUBICE

Newtonova trubice slouží k demonstraci nezávislosti tíhového zrychlení na hmotnosti tìlesa. Jedná se o sklenìnou trubici, která je natolik dobøe utìsnìná, že je z ní možné vyèerpávat vzduch. Nalézají se v ní pøedmìty rùzných hmotností. Vzduch vyèerpáme z trubice ve vertikální poloze, pak trubici rychle otoèíme o 180°. Pozorujeme padající tìlesa, která všechna padají volným pádem. Jejich rychlost postupnì roste, ale roste u všech tìles stejnì. Høebíèek i pírko dopadnou na dno trubice souèasnì. Pøírùstek rychlosti pro všechna volnì padající tìlesa v trubici s vakuem je stejný.

Mùžeme øíci, že tíhové zrychlení je pro všechna tìlesa ve vakuu stejné. Rychlost volnì padajících tìles je výraznì ovlivòována odporem vzduchu, nebo ve vakuu je pouze funkcí tíhového zrychlení a èasu.

2.2.VRH TÌLESA

Složitìjší pohyby konají tìlesa, jestliže jim udìlíme ve vakuu v homogenním tíhovém poli nenulovou poèáteèní rychlost . Pak je pohyb tìchto tìles složen ze dvou souèasných pohybù. Je to pøímoèarý pohyb ve smìru poèáteèní rychlosti a volný pád ve smìru tíhového zrychlení . Pro skládání tìchto dvou pohybù platí princip nezávislosti pohybù. Složením obou pohybù dostáváme složený pohyb, který nazýváme vrh tìlesa.

2.2.1.SVISLÝ VRH VZHÙRU

Svislý vrh vzhùru je rovnomìrnì zpomalený pohyb s poèáteèní rychlostí opaèného smìru, než je tíhové zrychlení . Okamžitá rychlost vrženého tìlesa se s rostoucí výškou zmenšuje. Pøi dosažení nejvyššího bodu trajektorie se rovná nule. Potom se tìleso vrací po téže trajektorii volným pádem k zemi. Trajektorií je èást svislé pøímky.

Animace prùbìhu svislého vrhu vzhùru

Velikost okamžité rychlosti tìlesa v èase t, mìøeném od poèátku pohybu, je dána vztahem

a okamžitá výška tìlesa y v èase t od poèátku pohybu vztahem

kde v₀t je dráha rovnomìrného pohybu konaného poèáteèní rychlostí ve smìru svisle vzhùru a dráha volného pádu.

Nejvìtší výšku, kterou mùže tìleso pøi svislém vrhu vzhùru dosáhnout, nazýváme výška výstupu h. V této výšce má vržené tìleso nulovou okamžitou rychlost ( v_h = 0 ). Po dosazení do vztahu pro okamžitou rychlost dostaneme výraz v₀ - gt_h = 0 a odtud získáme vztah pro dobu výstupu t_h = v₀/g. Dosadíme-li tuto dobu výstupu do vztahu pro okamžitou výšku y, dostáváme výšku výstupu

Z výšky h se tìleso vrací k zemi volným pádem. Doba jeho pádu je rovna dobì výstupu t_d = t_h a rychlost dopadu v_d= gv₀/g = v₀. Tìleso tedy dopadá na zem rychlostí, která má stejnou velikost jako poèáteèní rychlost, ale je opaèného smìru.

Mechanická energie pøi svislém vrhu vzhùru

Vržené tìleso má bìhem celého pohybu konstantní mechanickou energii, což znamená, že dochází k pøemìnì energie potenciální na kinetickou a naopak (zákon zachování mechanické energie). Pøi vržení má tìleso celkovou mechanickou energii rovnu kinetické energii, která se postupnì zmenšuje, pøemìnou v potenciální energii v tíhovém poli Zemì. V okamžiku dosažení maximální výšky výstupu má tìleso pouze potenciální energii. Potom dochází zpìt k pøemìnì potenciální energie v kinetickou energii a v okamžiku dopadu je celková mechanická energie opìt rovna kinetické energii.

2.2.2.VODOROVNÝ VRH

Vodorovný vrh koná tìleso, jemuž byla udìlena poèáteèní rychlost ve vodorovném smìru. Tento vrh vznikne složením rovnomìrného pøímoèarého pohybu ve vodorovném smìru a volného pádu ve svislém smìru. Jeho trajektorie je èást paraboly s vrcholem v místì vrhu.

Animace prùbìhu vodorovného vrhu

Zvolíme souøadnicovou soustavu Oxy a to tak, že souøadnice místa vrhu A jsou x₀ = 0, y₀ = 0 a poèáteèní rychlost má smìr osy x. Pak souøadnice bodu B, ve kterém se bude tìleso nacházet za dobu t od poèátku pohybu, budou

.

Nejvìtší vzdálenost od místa vrhu ve vodorovném smìru se nazývá délka vrhu d. Ve vzdálenosti d dokonèuje tìleso svùj pohyb, tedy v bodì D, který má souøadnice

x_D= d, y_D = 0.

Dosadíme toto do vztahu pro souøadnici , tzn.,

a vypoèítáme vztah pro dobu pohybu tìlesa, pomocí níž a vztahu pro souøadnici x = v₀t_d získáme délku vrhu

Ze vztahu plyne, že délka vrhu závisí pouze na poèáteèní rychlosti v₀ , kterou bylo tìleso vrženo a na výšce h, z níž bylo vrženo.

Zmìny rychlosti pøi vodorovném vrhu

V každém bodì trajektorie vodorovného vrhu je okamžitá rychlost tìlesa rovna vektorovému souètu rychlosti rovnomìrného pøímoèarého pohybu ve vodorovném smìru a rychlosti volného pádu ve svislém smìru.

VÝTOK KAPALINY OTVOREM V NÁDOBÌ

Mechanická energie tìlesa pøi vodorovném vrhu

Celková mechanická energie tìlesa je rovna souètu kinetické a potenciální energie. Na poèátku pohybu je tìlesu ve výšce h nad povrchem Zemì udìlena poèáteèní rychlost . Tìleso má v okamžiku vrhu obì složky mechanické energie nenulové. Pøi vodorovném vrhu tìlesa roste s èasem velikost okamžité rychlosti a zároveò dochází k pøírùstku kinetické energie a k úbytku potenciální energie tìlesa. V okamžiku dopadu tìlesa na zem je jeho celková mechanická energie rovna kinetické energii.

TAJEMSTVÍ VODOROVNÉHO VRHU

Vezmeme dvì kulièky a knihu, kterou držíme u stolu tak, aby mezi knihou a stolem vznikla mezera. Kulièky postavíme na stùl a pomocí pravítka, umístìného rovnobìžnì s hranou stolu, je souèasnì uvedeme do pohybu smìrem ke kraji stolu. Jedna z kulièek opustí stùl bez pøekážky a koná vodorovný vrh. Druhá kulièka však narazí do knihy a zaène padat volným pádem.

Z pokusu je vidìt, že obì kulièky dopadnou na zem souèasnì. Tento experiment potvrzuje, že svislá složka obou pohybù (vodorovného vrhu a volného pádu) je shodná, a že vodorovný vrh mùžeme chápat jako pohyb složený z volného pádu a dalšího pohybu ve smìru vodorovném. Tento druhý pohyb je rovnomìrný.

2.2.3.ŠIKMÝ VRH VZHÙRU

Šikmý vrh vzhùru je nerovnomìrný pohyb, který koná tìleso, je-li mu udìlena poèáteèní rychlost ve smìru, jenž svírá s vodorovnou rovinou úhel a . Úhel a se nazývá elevaèní úhel. Tento pohyb je výsledkem složení rovnomìrného pøímoèarého pohybu ve smìru rychlosti a volného pádu ve smìru zrychlení . Trajektorií pohybu je èást paraboly, jejíž vrchol je v nejvyšším bodì trajektorie.

Zvolíme-li souøadnicovou soustavu Oxy tak, že místo vrhu A má souøadnice x₀ = 0, y₀ = 0, pak souøadnice bodu B, v nìmž se tìleso ocitne v èase t od poèátku pohybu, budou

Pro délku vrhu d platí vztah .

Délka vrhu závisí na velikosti poèáteèní rychlosti v₀ a na elevaèním úhlu a . Pøi téže poèáteèní rychlosti je délka vrhu nejvìtší pro elevaèní úhel 45°.

Poznámka:

Pro zájemce uvádíme odvození vztahu pro délku vrhu.

Délku vrhu urèíme ze souøadnic bodu D. Pro ty platí x_D= d, y_D = 0, tedy . Pak pro dobu pohybu tìlesa platí t_d = 2v₀sina/g. Dosadíme-li do x_D = v₀t cosa , získáme hledanou délku vrhu .

V pøedchozích úvahách jsme pøedpokládali, že pohyb se dìje ve vakuu. Ve skuteènosti se však tìleso zpravidla pohybuje ve vzduchu. Vlivem odporu vzduchu se mìní rychlost pohybu (zmenšuje se) i tvar a délka trajektorie. Tìleso ve druhé polovinì trajektorie klesá k Zemi rychleji, výška výstupu i délka vrhu jsou menší, než by tomu bylo ve vakuu.

Šikmý vrh vzhùru má praktický význam zejména ve sportu a vojenské technice. Pøi støelbì ve vzduchu, kde se parabolická trajektorie deformuje pùsobením odporové síly na tzv. balistickou køivku, se dosahuje maximálního dostøelu pøi elevaèním úhlu 42°.

Mechanická energie pøi šikmém vrhu

Pøi šikmém vrhu vzhùru platí zákon zachování mechanické energie. V okamžiku poèátku vrhu je celková energie tìlesa rovna kinetické energii tìlesa a jeho potenciální energie je nulová. Bìhem pohybu se postupnì zmenšuje rychlost tìlesa a dochází k pøemìnì kinetické energie na potenciální energii tìlesa. V okamžiku, kdy tìleso dosáhne nejvìtší výšky vrhu, je celková mechanická energie tìlesa rovna potenciální energii. Pøi dalším pohybu tìlesa se pøemìòuje potenciální energie tìlesa v kinetickou energii a v okamžiku dopadu je jeho celková mechanická energie rovna kinetické energii tìlesa.

MODELOVÁNÍ TRAJEKTORIE ŠIKMÉHO VRHU VODNÍM PAPRSKEM

K ústí vodovodního kohoutku pøipojíme hadici a k ní ústí pøístroje pro demonstraci šikmého vrhu vodním paprskem. Na pøístroji pro demonstraci šikmého vrhu jsou vyznaèeny úhly ve stupních. Každý vodní paprsek znázoròuje trajektorii šikmého vrhu. Vidíme, jaká je délka vrhu pro rùzné velikosti elevaèních úhlù. Pustíme-li vodu ménì silným proudem, tzn. zmenšíme velikost poèáteèní rychlosti, budou délky jednotlivých vrhù menší, než pøi vìtší poèáteèní rychlosti a stejném elevaèním úhlu.

ØEŠENÁ ÚLOHA

V okamžiku, kdy jedno tìleso zaène padat volným pádem z výšky H = 30 m nad volným povrchem Zemì, je druhé tìleso vrženo svisle vzhùru rychlostí na povrchu Zemì.

Urèete velikost rychlosti druhého tìlesa tak, aby se setkalo s prvním tìlesem ve výšce h₂= 100 m nad Zemí.

Jaká bude pøi této rychlosti maximální výška výstupu druhého tìlesa ?

Øešení:

obr.

H = 300 m

h₂ = 100 m

h₁ = H - h₂ = 200 m

v₀ = ?

Pohyb prvního tìlesa je volný pád z výšky H = 300 m. Toto tìleso urazí do okamžiku setkání obou tìles vzdálenost h₁ = 200 m. Platí tyto vztahy

Þ ; v = g.t.

Druhé tìleso koná svislý vrh vzhùru s poèáteèní rychlostí . Pro jeho pohyb platí tyto vztahy

; v = v₀ - gt.

Doba, kterou potøebuje druhé tìleso k dosažení výšky h₁ je táž, jako doba, za niž první tìleso urazí dráhu h₂, tedy platí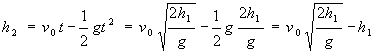

Odtud lze vypoèítat velikost poèáteèní rychlosti v₀ druhého tìlesa

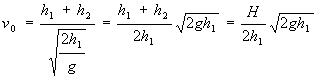Po dosazení v₀ = m.s^-1 = 47,43 m.s^-1

v₀ = 47,43 m.s^-1.

Pro maximální výšku výstupu druhého tìlesa platí vztah

Po dosazení h = m = 112,48 m

h = 112,48 m.

Velikost poèáteèní rychlosti druhého tìlesa je v₀ = 47,43 m.s^-1, jeho maximální výška výstupu je h = 112,48 m.

2.3. SHRNUTÍ - Pohyby tìles v homogenním tíhovém poli Zemì

Pohyb	Druh pohybu	Poèáteèní rychlost	Trajektorie	Charakteristické velièiny
volný pád	rovnomìrnì zrychlený pøímoèarý	nulová	èást pøímky	velikost okamžité rychlosti v = gt dráha
vrh svislý vzhùru	rovnomìrnì zpomalený pøímoèarý	nenulová, opaèného smìru než tíhové zrychlení	èást pøímky	velikost okamžité rychlosti v = v₀-gt okamžitá výška tìlesa výška výstupu h = v₀²/2g doba výstupu t_h = v₀/g
vodorovný vrh	nerovnomìrný, køivoèarý	nenulová, kolmá na vektor tíhového zrychlení	èást paraboly	souøadnice bodu trajektorie x = v₀t délka vrhu
šikmý vrh	nerovnomìrný, køivoèarý	nenulová, vektor rychlosti svírá s horizontálním smìrem elevaèní úhel a	èást paraboly	souøadnice bodu trajektorie délka vrhu

Test I.

Zpìt na obsah

Pokraèovat