podle t.
6.1 Skalární a vektorové pole
Teorii naleznete v kapitole 8.1 Multimediální encyklopedie nebo v kapitole 6.1 Breviáře
Příklad 1
Vypočtěte derivaci vektorového pole podle t.
Řešení
Derivace vektorového pole a(t) je definována analogicky jako derivace funkce f: R→R: 
. Zadané vektorové pole lze zapsat také jako 
, definujeme tedy funkci
a podle definice vypočteme
Derivaci můžeme vypočítat také přímo vestavěným příkazem pro derivaci
a podobně např. také hodnotu derivace v bodě t=4
Příklad 2
Bod se pohybuje tak, že v čase t je jeho polohový vektor r(t)=(cos t,sin t, t). Určete vektor okamžité rychlosti, vektor okamžitého zrychlení, velikost rychlosti a velikost zrychlení v čase t.
Řešení
Vektor okamžité rychlosti je derivací polohového vektoru podle času: 
. Vektor okamžitého zrychlení je derivací vektoru okamžité rychlosti (neboli druhou derivací polohového vektoru) podle času: 
. Velikost rychlosti a zrychlení je velikost vektoru okamžité rychlosti a okamžitého zrychlení.
První derivace polohového vektoru podle času (čili vektor rychlosti) je
Druhá derivace polohového vektoru podle času (čili vektor zrychlení) je
Velikosti jsou
a
Příklad 3
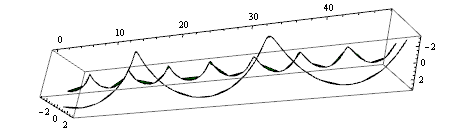
Po jaké křivce se pohybuje bod, jehož polohový vektor v čase t je r(t)=π(cos t,sin t, t)?
Řešení
Vektor r(t)=π(cos t,sin t, t) můžeme uvažovat jako součet dvou vektorů 
. Vektor 
odpovídá pohybu bodu po kružnici o poloměru π v rovině xy; vektor 
odpovídá pohybu bodu po ose z stálou rychlostí π. Složením těchto dvou pohybů vznikne šroubovice.
Doplňující otázka: v čem se liší šroubovice z příkladu 2 od šroubovice z tohoto příkladu?
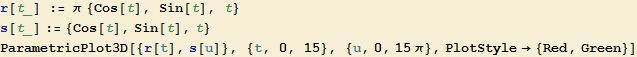
Příklad 4
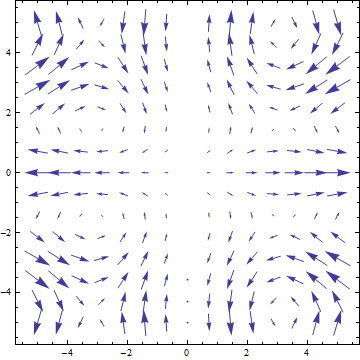
Znázorněte vektorové pole a(x,y)=(x cos y,y sin x) na množině <-5,5>×<-5,5>.
Řešení
Využijeme vestavěnou funkci VectorPlot:
