8.1 Skalární a vektorové pole 
Definice (skalárního pole)
Funkci
, definovanou
v určité oblasti 
, nazýváme
skalárním polem.
Poznámka
·
Skalární pole přiřazuje každému bodu oblasti 
určitou
číselnou hodnotu (skalár).
·
Používá se také zápis 
, kde
vektor 
.
·
V přírodních vědách je nejčastějším případem 
, kdy
nezávislé proměnné 
, 
, 
představují
kartézské souřadnice 
, 
, 
.
· Je zřejmé, že skalární pole můžeme parciálně derivovat podle jednotlivých proměnných stejně jako libovolnou matematickou funkci více proměnných.
Definice (hladiny skalárního pole)
Nadplochy[1] 
, tj.
nadplochy, na kterých je hodnota skalárního pole konstantní, nazýváme hladinami
tohoto pole.
Definice (vektorového pole)
Vektorovou funkci 
n
reálných proměnných, definovanou v určité oblasti 
, nazýváme
vektorovým polem (n proměnných)[2].
Poznámka
·
Vektorové pole přiřazuje každému bodu oblasti 
určitý
vektor 
, který
může mít libovolný počet složek. V dalším výkladu se však omezíme výlučně
na trojrozměrné vektory, které lze psát ve tvaru
.
Symboly 
, 
, 
představují
zde i dále v textu vektory ortonormální báze prostoru 
.
·
Počet proměnných n (tj. dimenze prostoru, na kterém je
vektorové pole definováno) bývá v praxi nejčastěji roven 1 nebo 3. Pro
můžeme
vektorové pole psát ve tvaru 
, kde
proměnná t mívá většinou význam času nebo délky oblouku křivky (pak
se obvykle značí s). V případě 
lze
použít zápis 
, kde
jsou
kartézské souřadnice a 
je
polohový vektor.
Definice (vektorové čáry)
Křivka, pro kterou platí, že tečna k ní má v každém jejím bodě směr vektoru vektorového pole v tomto bodě, se nazývá vektorovou čárou (siločárou).
Definice
Derivací vektorového
pole 
podle
proměnné t rozumíme vektorové pole
.
Poznámka
·
Derivují se všechny složky vektoru 
podle
proměnné 
, tzn.
je nutné provést tři obyčejné derivace.
· Zde i dále v textu necháváme stranou podmínky existence derivací apod. Předpokládáme, že všechny potřebné vlastnosti námi uvažovaná pole mají.
Příklad
·
Vektorové pole 
, kde
je
polohový vektor a 
je
čas, popisuje pohyb určitého bodu v čase. Derivace 
představuje
okamžitou rychlost tohoto bodu.
·
Častým případem je vektorové pole 
, kdy
parametrem s je délka oblouku křivky, kterou opisuje koncový bod polohového
vektoru 
.
Vektor 
pak
představuje jednotkový tečný vektor uvedené křivky v každém jejím bodě.
Věta
Pro derivaci součtu, násobku skalárem, skalárního součinu a vektorového součinu vektorových polí jedné proměnné platí věty analogické větám pro skalární funkce:
, 
, 
, 
.
Důkaz
Stačí rozepsat jednotlivá vektorová pole na složky a aplikovat věty o derivaci součtu a součinu skalárních funkcí.
Poznámka
Analogicky k definici (obyčejné) derivace vektorového pole jedné proměnné můžeme derivovat parciální derivace vektorového pole více proměnných. Např.
.
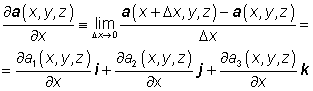