5.7 Plošný integrál druhého druhu
Teorii naleznete v kapitole 12.3 Multimediální encyklopedie nebo v kapitole 5.7 Breviáře
Příklad 1
Vypočítejte plošný integrál druhého druhu pole F(x,y,z) = [x,y,z] přes plochu s = [v cosu, v sinu, 2], kde u ∈ <0,2p> a v ∈ <0,1>.
Řešení
Plocha ze zadání tohoto příkladu je horní podstava válce o poloměru 1, s osou rovnoběžnou se souřadnicovou osou z a o výšce 2, tedy kruh o poloměru 1 ležící v rovině rovnoběžné se souřadnicovou rovinou xy a se středem v bodě [0,0,2].
Obecně plošný integrál druhého druhu počítáme pro zadané vektorové pole F, plochu s a pole jednotkových normálových vektorů n podle vzorce
,
kde na pravé straně uva žujeme znaménko "+", pokud je vektorový součin sloupců Jacobiho matice plochy s paralelní se zadaným polem jednotkových normálových vektorů n, a znaménko "-", pokud je antiparalelní.
Při výpočtu plošného integrálu druhého druhu musíme nejdříve definovat na zadané ploše pole jednotkových normálových vektorů.To určíme z vektorového součinu sloupců Jacobiho matice zadané plochy:
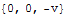
Máme tedy dvě možnosti: n1 = [0,0,-1] a n2 = [0,0,1]. V prvním případě je pole n1 paralelní s vektorovým součinem sloupců Jacobiho matice plochy s a na pravé straně výše uvedeného vzorce zvolíme pro toto pole znménko "+". Pole n2 je naopak s vektorovým součinem sloupců Jacobiho matice antiparalelní a na pravé straně vzorce musíme pro ně zvolit znaménko "-".
Výpočet integrálu na pravé straně je pak už nasnadě:
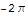
Pro volbu n1 je tedy příslušný plošný integrál roven -2π, pro volbu n2 pak 2π.
Na závěr si ještě pro úplnost vypišme mezivýsledky:
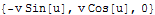
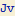
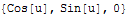
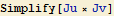
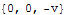
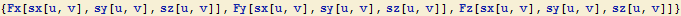
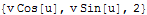
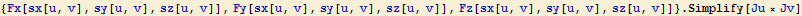
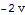
Příklad 2
Vypočítejte plošný integrál druhého druhu pole E =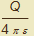 
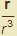, r = [x, y, z] přes povrch koule o poloměru R.
Řešení
Počítáme integrál přes uzavřenou plochu s = [R cosu sinv, R sinu sinv, R cosv], kde u ∈ <0,2p> a v ∈ <0,p>, jejíž jednotkový vektor vnější normály je paralelní s vektorovým součinem druhého a prvního (v tomto pořadí) sloupce Jacobiho matice s:
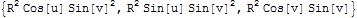
Ověříme to například tak, že vypočítáme složky tohoto vektorového součinu pro u = 0 a v = p/2(vzhledem ke spojitosti pole vek bude platit závěr učiněný pro tento vybraný bod
na celé ploše):
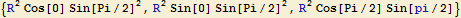
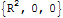
Plošný integrál pak počítáme následujícím postupem:
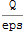
Porovnejte získaný výsledek s tvrzením Gaussovy věty elektrostatiky (pole E není totiž ničím jiným než elektrickou intenzitou elektrostatického pole buzeného nábojem Q umístěným v počátku souřadnicové soustavy).
