x.
3.9 Vybrané aplikace integrálního počtu
V matematice, ale zejména v přírodních a technických vědách, existuje nepřeberné množství problémů, kdy je nutné tím či oním způsobem použít výsledků integrálního počtu.
Teorii naleznete v kapitole 6.7 Multimediální encyklopedie nebo v kapitole 3.9 Breviáře
Příklad 1
Určete plochu vymezenou přímkami x = 0, x = π a křivkami y = sin x, x.
Řešení
Plocha je rovna rozdílu ploch pod oběma křivkami v intervalu < 0,π >. Tyto plochy lze určit vyčíslením určitých integralů v mezích 0 a π. Výsledná plocha je tedy:
(k výpočtu lze použít funkci Integrate)
Ze známé vlastnosti (aditivity) integrálů víme, že výpočet lze převést na výpočet jediného určitého integrálu z rozdílu obou funkcí:
Příklad 2
Lineární hustota ρ(x) = dm/dx tyče délky L je zadána funkcí ρ(x) = 
, kde x je vzdálenost od levého konce tyče. Určete celkovou hmotnost tyče m.
Řešení
Hmotnost elementu tyče délky dx v místě x je dm = ρ(x) dx. Celková hmotnost se určí "sečtením" elementů dm - to jest určitou integrací v mezích 0 a L.
Příklad 3
Určete momenty setrvačnosti homogenní tyče, jejíž hmotnost je M a délka L, a to vzhledem ke dvěma různým osám otáčení. V prvním případě vzhledem k ose procházející kolmo začátkem tyče a ve druhém případě těžištěm tyče.
Řešení
Moment setrvanosti elementu tyče dx je definován jako součin jeho hmotnosti dm a čtverce vzdálenosti od osy otáčení. Sečtením momentů setrvačnosti všech elementů (určitá integrace) dostaneme celkový moment setrvačnosti. V obou případech je lineární hustota konstantní ρ = (M / L).
V prvním případě (osa prochází koncem tyče), je vzdálenost elementu tyče dx od osy otáčení rovna x, provádíme součet momentů přes celou délku tyče, integrujeme tedy od 0 do L :
To je hledaný vztah pro moment setrvačnosti tyče v prvním případě.
Ve druhém případě rotuje tyč kolem těžiště. Jeho poloha je uprostřed tyče, tedy ve vzdálenosti 
= L/2. Označíme-li vzdálenost elementu tyče od těžiště y, a navíc si uvědomíme, že v této vzdálenosti se nachází dva takové elementy (jeden nalevo a druhý napravo od těžiště), můžeme součet momentů setrvačnosti jednotlivých elementů zapsat ve formě určitého integrálu v mezích od 0 do L/2.
Tím jsme obdrželi moment setrvačnosti tyče pro druhý případ.
Příklad 4
Určete moment setrvačnosti nehomogenní tyče z příkladu 2, vzhledem k ose procházející těžištěm kolmo k tyči.
Řešení
Nejdříve musíme určit polohu těžiště 
.
Podle definice musí platit, že 
.
Polohu těžiště můžeme tedy zapsat pomocí určitých integrálů:
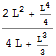
Označíme opět vzdálenost elementu tyče od těžiště y. I nyní máme vždy dva elementy tyče dx s touto vzdáleností, avšak každý z nich má jinou hmotnost, protože hustota tyče je nehomogenní. Moment setrvačnosti elementu je 
dm = 
ρ(x) dx. Celkový moment setrvačnosti tyče obdržíme jako součet těchto těchto momentů setrvačnosti podél celé délky tyče, tj.prostřednictvím určitého integrálu.
Tento integrál můžeme také vyjádřit obdobně jako v příkladu 2 (jedná se o substituci x = y + 
).
(V Mathematice je vhodné použít jinak pojmenované proměnné, např. xx a yy , aby nedošlo ke kolizi s předešlými definicemi, hodnota určitého integrálu tak jako tak nezávisí na označení integrační proměnné)
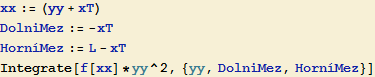
