+ 
= 4.5.1 Křivky
Spojitá křivka v n-rozměrném prostoru je zadána n-ticí spojitých reálných funkcí, které zavisí na jedné reálné proměnné a jsou definovány na vybraném intervalu a jejichž hodnoty reprezentují souřadnice bodu ležícícho na geometrickém obrazu této křivky. Jde tedy vlastně o spojitou vektorovou funkci jedné reálné proměnné označované jako parametr. Z tohoto důvodu hovoříme též o parametrickém zadání křivky. Konkrétní geometrický obraz křivky v prostoru může být určen odlišnými parametrickými zadáními, případně popsán v analytické formě pouze jako vztahy mezi jednotlivými souřadnicemi.
Teorii naleznete v kapitole 11.1 Multimediální encyklopedie nebo v kapitole 5.1 Breviáře.
Příklad 1
Parametrizujte a vykreslete křivku (tj. její geometrický obraz) ve dvou dimenzích, která je popsána rovnicí 2+ = 4.
Řešení
Křivku můžeme parametrizovat v závislosti na parametrui t následujícím způsobem.
Analytickou rovnici vydělíme 4, máme (1/2) 
+ (1/4) 
= 1, vzhledem k platnosti identity 
α + 
α = 1 tak můžeme předpokládat parametrické rovnice.
Takto definované funkce zatím ovšem závisí na dalších parametrech a, b a ω. Vzhledem k platnosti rovnic výše ale první dva nejsou nezávislé a musí platit:
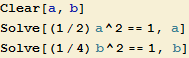
Můžeme tedy použít libovolnou kombinaci výše uvedených hodnot parametrů a a b, přičemž ω může mít hodnotu zcela libovolnou.
Protože funkce cos a sin jsou periodické s periodou 2π, bude křivka uzavřená neboť (cos (ω t) ,sin (ω t)) = (cos (ω t + 2π) ,sin (ω t + 2π)) a k jejímu plnému vykreslení postačí libovolný interval délky 2π / ω.
Zvolme tedy nejjednodušší a "nejpřirozenější" volbu parametrů a intervalu <c,d)
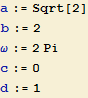
Parametrickou rovnici s těmito konkrétními hodnotami parametrů můžeme použít k vykreslení funkce.
(Mathematice umožňuje vykreslit 2D křivky pomocí funkce ParametricPlot)
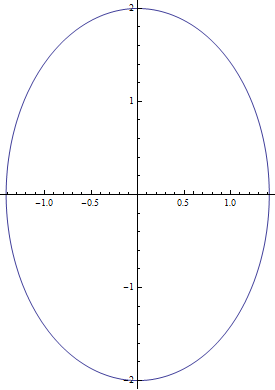
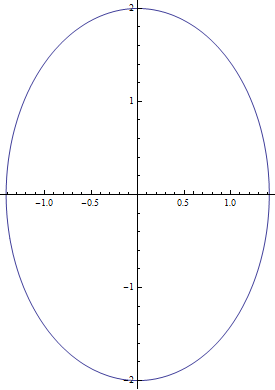
Vidíme, že se jedná o elipsu.
Tuto křivku můžeme popsat i jinými parametrickými rovnicemi, např.:
Vidíme, že se jedná o stejnou elipsu, přestože parametrické vyjádření je jiné.
Můžeme se pokusit vykreslit elipsu i s použitím analytické rovnice (Mathematica umožňuje vykreslit graf funkce - naši křivku ale musíme rozdělit na dvě funkce y(x) ):
Máme dvě řešení reprezentující dvě funkce. Ty odpovídají částem geometrického obrazu křivky pod resp. nad osou x.
(Graf funkce či více funkcí je možné v Mathematice vykreslit pomocí funkce Plot, abychom u křivky zachovali proporce, nastavujeme parametr AspectRatio)
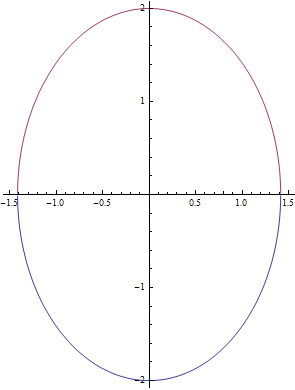
Příklad 2
Vykreslete křivky v rovině zadané parametrickými rovnicemi:
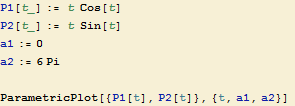
a) P1=t cos(t), P2=t sin(t)
b) Q1=t sin(t)cos(t), Q2=t 
(t)
pro t z intervalu <0,6π>.
Řešení
Definujeme zadane funkce parametru t (a vykreslíme křivky jako v předchozích případech).
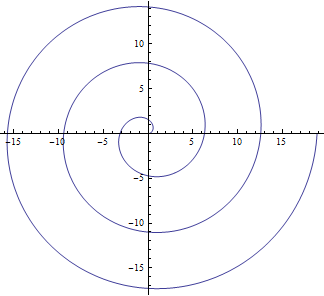
Křivka představuje spirálu.
Stejně to provedeme i ve druhém případě.
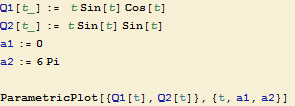
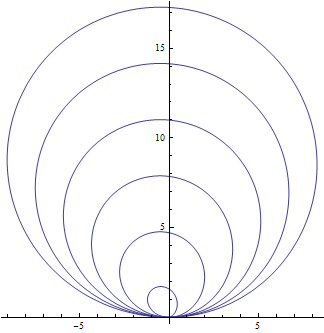
Tato křivka má již velmi zajímavý průběh.
Příklad 3
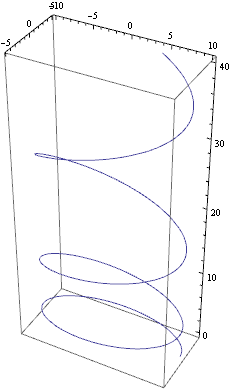
Vykreslete křivku definovanou ve třech dimenzích pomocí vektorové funkce
ψ =(10 cos(t), 5 sin(t), 
/10)
pro t z intervalu <0,20>.
Řešení
Postupujeme obdobně jako u křivek v rovině (definujeme tři funkce parametru t a vykreslíme křivku, tentokráte ale využijeme funkci ParametricPlot3D)
