6.2 Gradient

Teorii naleznete v kapitole 8.2 Multimediální encyklopedie nebo v kapitole 6.2 Breviáře

Příklad 1

Vypočtěte gradient skalárního pole u(r)==.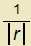

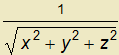Řešení

Gradient skalárního pole u je vektor gradu ≡ ∇u = 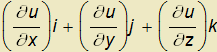≡ . Jedná se tedy o vektor, jehož složky jsou parciální derivace podle jednotlivých nezávislých proměnných funkce u.

a podle definice vypočteme jednotlivé parciální derivace:

Gradient skalárního pole je tedy vektor:

Gradient můžeme vypočítat také přímo vestavěným příkazem pro gradient skalárního pole (Ctrl+Shift+G):

Příklad 2

Nalezněte směr (vektor), ve kterém hodnota funkce

u(r)=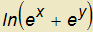 v bodě [4,2] roste nejrychleji.

Řešení

Gradient určuje směr, v němž funkce roste nejrychleji, stačí tedy vypočítat gradient funkce u(r).

Po vyčíslení:

Směr vektoru se nezmění, násobíme-li ho nezáporným reálným číslem; nalezený vektor tedy můžeme např. normovat:

Příklad 3

Vypočtěte ∇u(r), je-li u(r)= a =.

Řešení

Uvážíme-li, že u(r)= a = (viz zadání), můžeme výsledek přepsat do tvaru =.

Příklad 4

Vypočtěte |∇(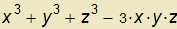)(2,1,1)|.

Řešení

Úlohou je určit velikost gradientu funkce 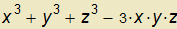v bodě [2,1,1].