Teorii naleznete v kapitole 8.5 Multimediální encyklopedie nebo v kapitole 6.5 Breviáře
Aplikujte Laplaceův operátor na skalární pole
u(r)=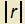 =
=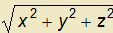 .
.
Laplaceův operátor je operátor ∆≡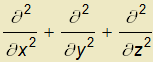 ≡∇∙∇=
≡∇∙∇=
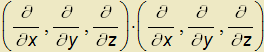 . Aplikujeme-li tento operátor na skalární pole u, získáme
. Aplikujeme-li tento operátor na skalární pole u, získáme
∆u≡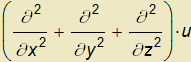 =
=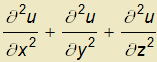 , čili opět skalární pole. Výpočet provedeme jako součet druhých parciálních derivací podle jednotlivých nezávisle proměnných (kartézských souřadnic):
, čili opět skalární pole. Výpočet provedeme jako součet druhých parciálních derivací podle jednotlivých nezávisle proměnných (kartézských souřadnic):
Neboli
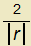 .
.
Jelikož Mathcad nemá vestavěnou funkci pro Laplaceův operátor, můžeme si ho zadefinovat sami:
Nebo můžeme mírně upravit předtím zavedený operátor a opět vypočíst:
Výsledek lze zapsat též ve tvaru
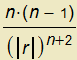 .
.
Aplikujte Laplaceův operátor na vektorové pole a(r)=r=(x,y,z).
Aplikace Laplaceova operátoru ∆≡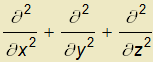 na vektorové pole a je definovana jako
na vektorové pole a je definovana jako
∆a=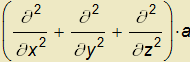 =
=
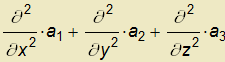 .
.
Výsledkem je tedy opět vektorové pole. Výpočet provedeme aplikací Laplaciánu na jednotlivé složky vektorového pole a.
Nebo si také můžeme definovat vlastní Laplaceovu funkci pro vektorové pole:
Aplikujte Laplaceův operátor na vektorové pole a(r)=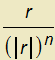 , kde r=(x,y,z) a
, kde r=(x,y,z) a
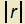 je délka vektoru r.
je délka vektoru r.
Výpočet přímo podle definice provedeme známým postupem:
Nebo si opět můžeme definovat vlastní Laplaceovu funkci pro vektorové pole s jedním parametrem:
Výsledek lze zapsat také ve tvaru
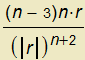 .
.
≡∇∙∇=
. Aplikujeme-li tento operátor na skalární pole u, získáme
=
, čili opět skalární pole. Výpočet provedeme jako součet druhých parciálních derivací podle jednotlivých nezávisle proměnných (kartézských souřadnic):