5.9.1 Lokální extrémy funkce dvou reálných proměnných

Nechť má funkce f(x,y) v bodě a = [a_x,a_y] obě první parciální derivace nulové,

.

Pak v tomto bodě může studovaná funkce nabývat lokálního extrému. Konečné rozhodnutí, zda tomu tak je, a rozhodnutí o povaze extrému závisí na chování kvadratické formy

,

kde

,    a  .

O její pozitivní či negativní definitnosti rozhodneme na základě znamének vlastních čísel matice A_ij.  Odpovídající charakteristická rovnice nabývá tvaru

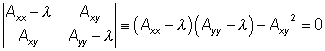
a po úpravách

.

Jedná se tedy o kvadratickou rovnici s neznámou  l,  pro jejíž kořeny můžeme psát podle obecného vzorce

.

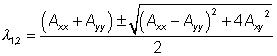Všimněte si především, že obě vlastní čísla jsou nutně reálná, výraz pod odmocninou je totiž vždy nezáporný. Podle jejich znamének pak již můžeme snadno usoudit na typ extrému:

·        jsou-li obě vlastní čísla kladná, je odpovídající kvadratická forma pozitivně definitní a funkce f má v zadaném bodě lokální minimum,
·        jsou-li obě vlastní čísla záporná, je odpovídající kvadratická forma negativně definitní a funkce f má v zadaném bodě lokální maximum,
·        mají-li obě vlastní čísla různá znaménka, je odpovídající kvadratická forma indefinitní a funkce f nemá v zadaném bodě lokální extrém.

Je-li alespoň jedno z vlastních čísel nulové, nelze o povaze extrému ani o tom, zda jej funkce f  v bodě  a  skutečně nabývá, ze samotných druhých derivací rozhodnout.