3.1 Davissonův - Germerův pokus
Metoda
Samotná de Broglieho hypotéza předpokládající za jistých okolností vlnové chování částic je v rámci klasické fyziky natolik neobvyklá, že by byla bez experimentálního potvrzení zajisté zavržena. S trochou nadsázky můžeme proto říci, že jí pevné místo v rámci moderní fyziky zajistila teprve Davissonova, Germerova a Thomsonova měření.
Jak ovšem vlnové chování klasických částic experimentálně prokázat? Inspiraci mohli zmínění experimentátoři hledat, a taky najít, v optice první poloviny 19. století. Tehdy se totiž podařilo nade vši pochybnost prokázat vlnové vlastnosti světla prostřednictvím jeho ohybu (difrakce) na malých aperturách (viz např. slavný experiment Youngův).
To ovšem může být technicky velmi obtížné, protože ohybové (difrakční) jevy pozorujeme v optice jen tehdy, je-li charakteristický rozměr soustavy, na níž difrakci hodláme pozorovat - např. mřížková konstanta - srovnatelný s vlnovou délkou použitého záření.
Předpokládáme, že stejné omezení zůstává v platnosti i pro vlny de Broglieho. Proto si nejdříve udělejme alespoň namátkovou inventuru vlnových délek, které můžeme podle de Broglieho hypotézy u některých těles očekávat.
|
Objekt |
Rychlost [m/s] |
Hmotnost [kg] |
De Broglieho vlnová délka [m] |
|
běžící člověk |
2 |
70 |
|
|
zrnko písku |
1 |
|
|
|
molekula dusíku |
502 |
|
|
|
proton |
|
|
|
|
elektron |
|
|
|
(a) Molekula
dusíku pohybující rychlostí odpovídající střední kvadratické rychlosti molekul
v plynu při teplotě 300 K, (b) proton urychlený potenciálovým rozdílem 10 V,
(c) elektron urychlený potenciálovým rozdílem 10 V.
Z uvedené tabulky, jakkoliv neúplné, je zřejmé, že de Broglieho vlnové délky přiřazené makroskopickým objektům (A, B) jsou beznadějně malé na to, abychom pro ně vůbec nějakou difrakci mohli pozorovat. I pro těžší objekty mikrosvěta (molekuly, atomy či protony) jsou získané vlnové délky velmi malé. K pozorování difrakce bychom museli mít v případě těchto objektů k dispozici příliš jemnou mřížku.
Naopak poměrně příznivá situace nastává pro lehké, nepříliš urychlené elektrony. Jejich vlnové délky totiž odpovídají zhruba vzdálenostem krystalických rovin v krystalech pevných látek. Přímo se proto nabízí možnost pokusit se pozorovat difrakci lehkých elektronů na krystalických rovinách vhodně zvoleného monokrystalu. Tato idea nebyla koneckonců v roce 1927 nová. Již dříve ji využil německý fyzik Max von Laue k důkazu vlnového charakteru Röntgenových paprsků X.
Experiment
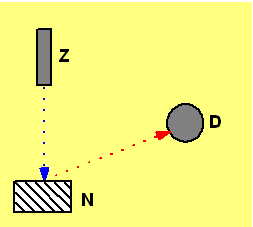Davisson
a Germer pozorovali difrakci elektronů na krystalických rovinách monokrystalu
niklu. Elektronovým dělem Z ozařovali ve vysokoteplotní peci vyžíhaný
monokrystal niklu N a detektorem D
měřili počet odražených elektronů v různých směrech. A získali velmi
zajímavé výsledky: Kromě výrazného a v rámci částicové interpretace dobře
pochopitelného maxima počtu elektronů odražených od povrchu krystalu ve směru
zpět k elektronovému dělu pozorovali
navíc i další maximum. To souviselo s difrakčními efekty.
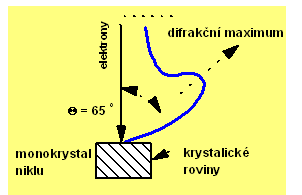Velmi
zřetelné bylo toto maximum pro elektrony urychlené potenciálovým rozdílem 54 V,
kdy se elektrony odrážely, jak ukazuje připojený obrázek, s převahou do
směru svírajícího s krystalovými rovinami monokrystalu niklu úhel 
Tomuto výraznému
ohybovému maximu odpovídá vlnová délka dopadajících elektronů 
Z experimentálních
dat ji můžeme vypočítat, zanedbáme-li výstupní práci krystalu niklu, z Braggovy
rovnice
v níž položíme řád difrakčního maxima N =
1 a kde
a je vzdálenost krystalových rovin v
monokrystalu niklu (0,091 nm) a q výše uvedený úhel. Podle de Broglieho teorie
je vlnová délka elektronu urychleného na energii 
rovna 
což je ovšem v
dokonalé shodě s hodnotou experimentální.
Rozšíření experimentu
Difrakce na krystalických mřížkách byla pozorována nejen pro elektrony, ale i pro těžší částice. Tak např. v roce 1930 němečtí fyzikové Esterman, Frisch a Stern pozorovali difrakční efekty pro atomy helia bombardující monokrystal fluoridu lithia (LiF) a později Mitchell a Powers i pro neutrony bombardující monokrystal oxidu hořečnatého (MgO) [4].
[1] DAVISSON,
C. and GERMER, LH. Physical Review,
1927, vol. 30, p. 705.
[2] THOMSON, GP. and REID, A. Nature, 1927, vol. 119, p. 890.
[3] THOMSON, GP. Proceedings of the Royal Society of London, 1928, vol.
117, p. 600.
[4] MITCHELL, DP. and POWERS, PN. Physical Review, 1936, vol. 50, p. 486.
[5] HAJKO, V., aj. Fyzika v experimentoch. 1. vyd. Bratislava: Veda, 1988. 415 s.
s. 70-75.
[6] BEISER, A. Úvod do moderní fyziky. 1. vyd. Praha: Academia, 1978. 628 s. s. 100-104.
