Kritický stav látky a rovnice van der Waalsova

Vyšetříme nyní, do jaké míry vyjadřuje stavová rovnice van der Waalsova

toto chování soustavy kapalinapára. Přepíšeme rovnici (1) na tvar

Považujme tuto rovnici za vztah mezi p a V, přičemž T je parametr. Při konstantním T lze pak k danému tlaku p vypočíst objem V. Protože rovnice (3,2,4,5,2) je třetího stupně, existují k danému p obecně tři kořeny V. Je-li , ukazuje se, že dva z nich jsou komplexně sdružené, třetí je reálný kladný. Jinými slovy, v tomto příkladě protíná přímka p = konst. izotermu v jediném bodě: danému tlaku přísluší zcela určitý objem.

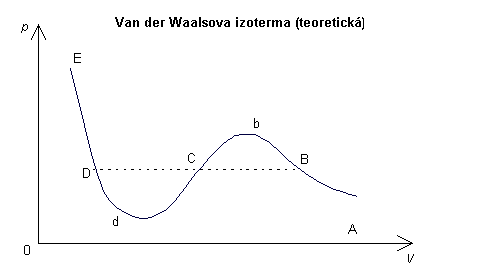
Jestliže je však, má rovnice (3,2,4,5,2) všechny tři kořeny reálné různé. Průběh izotermy je v tomto případě dán křivkou v grafu 12. Přímka p = konst. protíná tuto křivku ve třech bodech D, C, B. V úsecích AB a DB izoterma v grafu 11, získána experimentálně, se kryje s izotermou v grafu 12 z rovnice van der Waalsovy. Teoretická křivka má v úseku BD maximum b v a minimum v d. Část křivky Bb odpovídá přechlazení páry, k němuž dojde, nejsou-li v páře kondenzační jádra. Úsek Dd odpovídá pak přechlazení kapaliny. Oba tyto jevy byly pozorovány, úsek křivky bCd dosud pozorován nebyl. Stavy mezi B a D nejsou však stabilní, proto přecházejí obvykle ihned v rovnovážný stav (děj) daný úsečkou BCD.

Graf 12

Zbývá ještě určit polohu kritického bodu K. Podle grafu 11 je to bod při němž všechny tři reálné průsečíky C, D, B splynou v jediný. Rovnice (3,2,4,5,2) má při trojný kořen . Kubickou rovnici s trojným kořenem lze však převést na tvar

nebo-li

Srovnáním koeficientů rovnic (3,2,4,5,2) a (3,2,4,5,3) plyne

Jejich řešením obdržíme

Známe-li hodnoty konstant a, b rovnice van der Waalsovy, lze z rovnic (3,2,4,5,5) vypočíst hodnoty pro kritický stav.