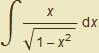.
3.3 Integrace substitucí
Teorii naleznete v kapitole 6.3 Multimediální encyklopedie nebo v kapitole 3.3 Breviáře
Příklad 1
Pomocí první věty o substituci vypočítejte .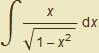
Řešení
První věta o substituci zní:
∫f(g(x))g´(x)dx = 
V integrandu zadaného integrálu tedy musíme rozpoznat součin dvou funkcí, z nichž jedna je složená a to tak, že když zderivuji její vnitřní funkci, obdržím funkci druhou.
V našem případě bude nutná malá úprava integrandu:
= 
(-2x).
Odtud f(y) = 
, g(x) = 
a g´(x) = -2x.
Nyní můžeme podle první věty o substituci psát: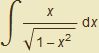
= 
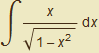
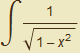(-2x)dx = 
.
Integrál 
je velmi jednoduchý, přesto, můžeme jej vypočítat pomocí programu Mathematica.
Teď již stačí jen dosadit:
Tento postup odpovídá běžnému výpočtu integrálu substituční metodou bez matematickeho software.
Mathematica umí integrál vypočítat rovnou:
Příklad 2
Pomocí druhé věty o substituci vypočítejte 
.
Řešení
Druhá věta o substituci zní:
∫f(x)dx = ∫f(h(t))h´(t)dt, kde
x = h(t),
t = 
(x),
dx = h´(t)dt.
Nejobtížnějším krokem je volba substituce x = h(t).
V našem pípadě povede k cíli volba
t = 
,
x = at,
dx = a dt.
Pak lze integrál přepsat do tvaru 
=
= 
. Tento integrál bychom měli znát zpaměti, můžeme ale i pro jeho výpočet použít program Mathematica .
Pak již stačí pouze dosadit substituci x = at.
Mathematica ovšem umí nalézt správnou substituci sama, proto lze integrovat rovnou:
Příklad 3
Vypočítejte 
dx
Řešení
Volba správné substituce je zde velmi obtížná. V tomto případě vede k cíli substituce x =
.
Výpočet pomocí programu Mathematica je však velmi jednoduchý:
Příklad 4
Vypočítejte 
dx
Řešení
Opět, nejobtížnějším krokem je volba správné substituce. V tomto případě vede k cíli substituce x = 2cos t. Dále se již jedná o rutinní výpočet.
Vypočet pomocí programu Mathematica :
