1.4 Průběh funkce
Často potřebujeme získat celkovou představu, jak zadaná funkce závisí na své nezávislé proměnné - vyšetřit její průběh. Konečným cílem takového snažení pak obvykle bývá náčrt grafu zkoumané funkce.
Teorii naleznete v kapitole
4.6 Multimediální encyklopedie nebo v kapitole
1.4 Breviáře
Příklad 1
Vyšetřete průběh funkce
Řešení
Definujme funkci (viz definice funkce)
Protože výraz je vždy nenulový, je maximální definiční obor studované funkce totožný s množinou všech reálných čísel.
Průsečík s osou y (x = 0, stačí spočítat funkční hodnotu):
Průsečík s osou x (y = 0, řešíme rovnici pro neznámou x, pomocí funkce Solve ):
Funkce je spojitá na množině všech reálných čísel, neboť obě funkce x a 
jsou spojitými funkcemi a druhá znich nenabývá navíc v žádném bodě reálné osy nulové hodnoty.
Limita v minus nekonečnu (pomocí funkce Limit):
Limita v plus nekonečnu (opět funkce Limit):
Intervaly monotonie:
Intervaly monotonie hledáme řešením nerovnic 
resp. 
.
Potřebujeme tedy znát první derivaci studované funkce (spočteme použitím funkce D a zjednodušíme ji pomocí Simplify)
Pro rostoucí funkci je derivace kladná a pro klesající záporná, body (tzv. stacionární body, či obecně oblasti), kde dochází ke změně znaménka, odpovídají nulové derivaci. Tyto body určíme řešením příslušné rovnice.
Kladná derivace resp. záporná derivace určí intervaly, kde je funkce monotónně rostoucí resp. klesající (využijeme funci Reduce k vyřešení příslušných nerovnic):
Na intervalu (-1,1) je tedy funkce f rostoucí, na intervalech (-∞,-1) a (1,∞) klesající.
Lokální extrémy
Na základě právě určených intervalů monotonie vidíme okamžitě, že v bodě x = -1 nabývá studovaná funkce svého lokálního minima a v bodě x = 1 lokálního maxima. Výše jsme již ukázali, že jsou to staconární body s nulovou první derivací. O tom, zda je v těchto bodech extrém (minimum či maximum) rozhodne druhá derivace funkce (můžeme derivovat 1. derivaci opět pomoci funkce D nebo zadat výpočet druhé derivace původní funkce f(x) rozšířením parametru funkce D na {x, 2}).
V případě minima je druhá derivace kladná:
V případě maxima je druhá derivace záporná:
(V Mathematice lze hodnotu či hodnoty výrazu nebo funkce, zde derivace, v daném bodě určit také přímo pomocí operátoru /.)
(Ve výše uvedené formě se ale derivace pokaždé počítá znovu)
Intervaly konvexnosti a konkávnosti
Musíme zjistit, pro které intervaly má druhá derivace funkce kladnou (konvexní funkce) resp. zápornou hodnotu (konkávní funkce).
(Využit lze i zde funkci Reduce pro řešení příslušných nerovnic).
Pro první dvojici spočtených intervalů je funkce konvexní pro druhou konkávní.
Asymptoty
Přímky 
, k nimž se graf funkce v plus či minus nekonečnu neomezně blíží.
Asymptota v -∞
Parametry určíme pomocí limity.
Parametr k1
Parametr q1
Tedy y = 0 - asymptotou je osa x.
Asymptota v ∞
Parametry určíme podobným způsobem.
Parametr k2
Parametr q2
Opět y = 0 - i zde je asymptotou je osa x.
Graf funkce
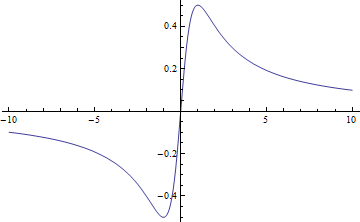
Nakonec můžeme vykreslit graf funkce např. na intervalu (-10,10).
(využijeme funkci Plot s možností nastavení požadovaného intervalu).
