5.6 Derivace ve směru

Parciální derivace   popisuje, jak se v zadaném bodě mění funkce  f  podél k-té souřadnicové osy. V této kapitole si ukážeme, jak popsat změnu dané funkce podél libovolné přímky procházející bodem  a.

Definice

Nechť    je jednotkový vektor, tj. platí [1]. Pak limitu

nazveme derivací funkce  f  v bodě a ve směru  n.  Budeme pro ni používat symbol .

Poznámka

Pro speciální volbu  ,  kde jednička stojí na k-té pozici a vektor  n  míří ve směru k-té souřadnicové osy, přechází derivace v zadaném směru na prostou parciální derivaci:

.

Věta

Nechť funkce  f  má na nějakém okolí bodu  a  všechny první parciální derivace, které jsou navíc v bodě  a  spojité. Pak platí

,

kde    jsou složky vektoru  n.

Definice

Vektor

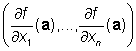
nazýváme gradientem funkce  f  v bodě  a.  Obvykle pro něj používáme označení  [2].

Poznámka

Pomocí gradientu můžeme vzorec pro výpočet derivace ve směru  n  přepsat do stručnějšího a přehlednějšího tvaru

.

Současně však můžeme zapsat skalární součin dvou vektorů jako součin jejich velikostí a kosinu úhlu, který svírají. Platí tedy

,

kde  a  je úhel sevřený vektorem gradientu   a jednotkovým vektorem  n,  .  Derivace    bude proto nabývat své maximální hodnoty pro  .  Můžeme tedy říci, že gradient funkce zadává směr jejího maximálního růstu.

[1] Symbolem || || označujeme eukleidovskou normu vepsaného vektoru (viz též zde).