 Skládání rovnoběžných kmitů Skládání rovnoběžných kmitů
|
Princip superpozice |
Skládání kmitání graficky | Skládání kmitání
stejné a
různé frekvence
 Okamžitou výchylku hmotného bodu, který zároveň koná více kmitů stejného směru, získáme pomocí principu superpozice:
Okamžitou výchylku hmotného bodu, který zároveň koná více kmitů stejného směru, získáme pomocí principu superpozice:
Jestliže hmotný bod koná současně několik harmonických pohybů téhož směru s okamžitými výchylkami y1, y2 , . . . , yk, je okamžitá výchylka y výsledného kmitání
y = y1 + y2 + . . . + yk.Okamžité výchylky mohou mít kladnou i zápornou hodnotu. |
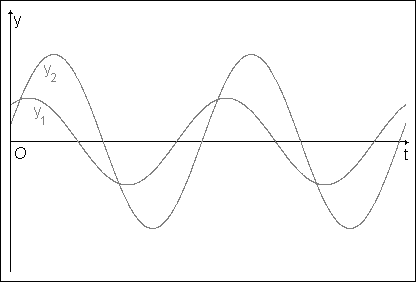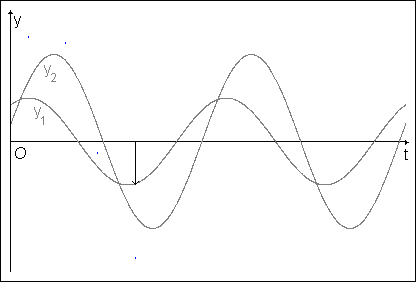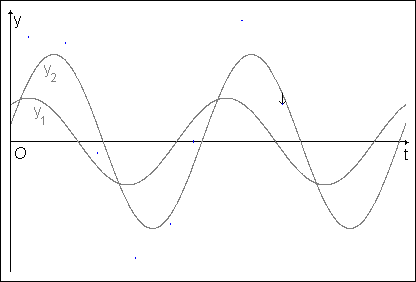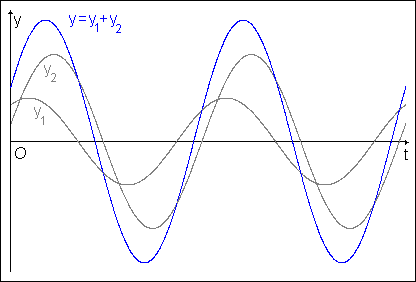
 Na následujícím obrázku 1 jsou znázorněny časové diagramy dvou harmonických kmitů stejné frekvence. Je zde ukázán grafický postup, kterým můžeme získat časový diagram složeného kmitání (y = y1 + y2). Sečteme, popř. odečteme délky úseček odpovídající okamžitým výchylkám v jednotlivých okamžicích s přihlédnutím ke znaménku výchylky. Křivka proložená koncovými body součtů úseček určuje časový průběh složeného kmitání.
Na následujícím obrázku 1 jsou znázorněny časové diagramy dvou harmonických kmitů stejné frekvence. Je zde ukázán grafický postup, kterým můžeme získat časový diagram složeného kmitání (y = y1 + y2). Sečteme, popř. odečteme délky úseček odpovídající okamžitým výchylkám v jednotlivých okamžicích s přihlédnutím ke znaménku výchylky. Křivka proložená koncovými body součtů úseček určuje časový průběh složeného kmitání.
|
|
Obr. 1 Grafický postup při skládání dvou rovnoběžných kmitů.
|
 Časový průběh okamžité výchylky složeného kmitání závisí na amplitudě výchylky, frekvenci a fázovém rozdílu složek. Tuto závislost nyní vyšetříme pro případ skládání dvou kmitání. Za základní vezmeme dělení podle frekvence: buď f1= f2 nebo f1
Časový průběh okamžité výchylky složeného kmitání závisí na amplitudě výchylky, frekvenci a fázovém rozdílu složek. Tuto závislost nyní vyšetříme pro případ skládání dvou kmitání. Za základní vezmeme dělení podle frekvence: buď f1= f2 nebo f1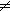 f2.
f2.
 Kliknutím na obrázky 2 až 5 spustíte modely dané situace v programu Famulus.
Kliknutím na obrázky 2 až 5 spustíte modely dané situace v programu Famulus.
 1. Skládáním dvou harmonických kmitání o stejné frekvenci (f1= f2) vzniká opět harmonické kmitání téže frekvence. Jeho amplituda výchylky závisí na fázovém rozdílu skládaných kmitání. Mohou nastat tyto možnosti.
1. Skládáním dvou harmonických kmitání o stejné frekvenci (f1= f2) vzniká opět harmonické kmitání téže frekvence. Jeho amplituda výchylky závisí na fázovém rozdílu skládaných kmitání. Mohou nastat tyto možnosti.
- Skládaná kmitání mají stejnou fázi (Dj = 2kp, k-celé číslo, obr. 2). Složené kmitání má stejnou počáteční fázi jako složky a pro amplitudu složeného kmitání platí
ym = ym1+ ym2
Amplituda výchylky je v tomto případě největší.
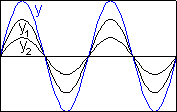
- Skládaná kmitání mají opačnou fázi (Dj = (2k+1)p, k-celé číslo, obr. 3). Složené kmitání má stejnou počáteční fázi jako složka s větší amplitudou výchylky a pro amplitudu výchylky složeného kmitání platí
ym = | ym1- ym2 |
Amplituda výchylky je v tomto případě nejmenší.
- Ostatní fázové rozdíly skládaných kmitání. Pro velikost amplitudy výchylky složeného kmitání platí
| ym1- ym2 | < ym < ym1+ ym2
 |
 |
| Obr. 2 | Obr. 3 |
 2. Skládáním dvou harmonických kmitání různé frekvence (f1
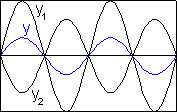
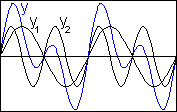
2. Skládáním dvou harmonických kmitání různé frekvence (f1 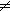 f2) vzniká složené kmitání které není harmonické. Na obr. 4 je diagram složeného kmitání, jehož složky mají stejnou amplitudu výchylky i počáteční fázi a jejich frekvence jsou v poměru 1:2.
f2) vzniká složené kmitání které není harmonické. Na obr. 4 je diagram složeného kmitání, jehož složky mají stejnou amplitudu výchylky i počáteční fázi a jejich frekvence jsou v poměru 1:2.
- Zajímavý případ nastane, jestliže skládáme kmitání s blízkými frekvencemi (např. 1 Hz a 1,1 Hz). Vzniká složené kmitání s charakteristickým průběhem, které nazýváme rázy, obr. 5.
 |
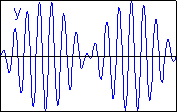 |
| Obr. 4 | Obr. 5 |

| Vznik rázů pomocí dvou mírně rozladěných ladiček.
|
| Skládání dvou rovnoběžných kmitů. Můžete zadat frekvence těchto kmitů (f1, f2), jejich amplitudy (A1, A2) a fázový rozdíl kmitů (fi)
|

| Ověřte si své znalosti!
|
 Skládání rovnoběžných kmitů
Skládání rovnoběžných kmitů Skládání rovnoběžných kmitů
Skládání rovnoběžných kmitů Okamžitou výchylku hmotného bodu, který zároveň koná více kmitů stejného směru, získáme pomocí principu superpozice:
Okamžitou výchylku hmotného bodu, který zároveň koná více kmitů stejného směru, získáme pomocí principu superpozice: Na následujícím obrázku 1 jsou znázorněny časové diagramy dvou harmonických kmitů stejné frekvence. Je zde ukázán grafický postup, kterým můžeme získat časový diagram složeného kmitání (y = y1 + y2). Sečteme, popř. odečteme délky úseček odpovídající okamžitým výchylkám v jednotlivých okamžicích s přihlédnutím ke znaménku výchylky. Křivka proložená koncovými body součtů úseček určuje časový průběh složeného kmitání.
Na následujícím obrázku 1 jsou znázorněny časové diagramy dvou harmonických kmitů stejné frekvence. Je zde ukázán grafický postup, kterým můžeme získat časový diagram složeného kmitání (y = y1 + y2). Sečteme, popř. odečteme délky úseček odpovídající okamžitým výchylkám v jednotlivých okamžicích s přihlédnutím ke znaménku výchylky. Křivka proložená koncovými body součtů úseček určuje časový průběh složeného kmitání.
 Časový průběh okamžité výchylky složeného kmitání závisí na amplitudě výchylky, frekvenci a fázovém rozdílu složek. Tuto závislost nyní vyšetříme pro případ skládání dvou kmitání. Za základní vezmeme dělení podle frekvence: buď f1= f2 nebo f1
Časový průběh okamžité výchylky složeného kmitání závisí na amplitudě výchylky, frekvenci a fázovém rozdílu složek. Tuto závislost nyní vyšetříme pro případ skládání dvou kmitání. Za základní vezmeme dělení podle frekvence: buď f1= f2 nebo f1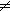 f2.
f2.  Kliknutím na obrázky 2 až 5 spustíte modely dané situace v programu Famulus.
Kliknutím na obrázky 2 až 5 spustíte modely dané situace v programu Famulus. 1. Skládáním dvou harmonických kmitání o stejné frekvenci (f1= f2) vzniká opět harmonické kmitání téže frekvence. Jeho amplituda výchylky závisí na fázovém rozdílu skládaných kmitání. Mohou nastat tyto možnosti.
1. Skládáním dvou harmonických kmitání o stejné frekvenci (f1= f2) vzniká opět harmonické kmitání téže frekvence. Jeho amplituda výchylky závisí na fázovém rozdílu skládaných kmitání. Mohou nastat tyto možnosti.


 2. Skládáním dvou harmonických kmitání různé frekvence (f1
2. Skládáním dvou harmonických kmitání různé frekvence (f1 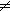 f2) vzniká složené kmitání které není harmonické. Na obr. 4 je diagram složeného kmitání, jehož složky mají stejnou amplitudu výchylky i počáteční fázi a jejich frekvence jsou v poměru 1:2.
f2) vzniká složené kmitání které není harmonické. Na obr. 4 je diagram složeného kmitání, jehož složky mají stejnou amplitudu výchylky i počáteční fázi a jejich frekvence jsou v poměru 1:2.

