Na obrázku 1.A je časový diagram kmitavého pohybu o rovnici y = y_msin wt. Na obrázku 1.B je ale časový diagram kmitavého pohybu, jehož výchylka v čase t = 0 je nenulová, v našem případě y(0) = y_m/2.

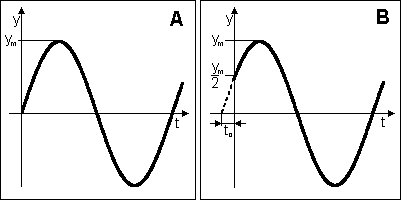Obr. 1: Na pravém obrázku nenulová počáteční fáze.

Jaký tvar bude mít rovnice kmitavého pohybu v tomto obecném případě ? Kmitající těleso procházelo rovnovážnou polohou o čas t₀ dříve. Rovnice harmonického kmitání bude mít tedy tvar:

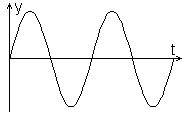
Následující obrázky ukazují časové diagramy kmitavého pohybu pro některé hodnoty počáteční fáze.

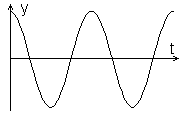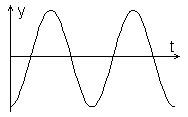
j0 = 0 rad	j0 = p/2 rad
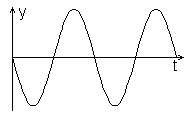j0 = -p/2 rad	j0 = p rad

Počáteční fáze je důležitá pro posouzení vzájemných vztahů fyzikálních veličin kmitavého pohybu. Obvykle vyjadřujeme fázový rozdíl těchto veličin. Jesliže dvě harmonické veličiny mají stejnou úhlovou frekvenci a počáteční fáze j₀₁ a j₀₂, platí pro fázový rozdíl Dj:

Jestliže přepíšeme rovnice kinematických veličin harmonického kmitání,
y = y_msin wt
v = wy_mcos wt = wy_msin (wt+p/2)
a = -w²y_msin wt = w²y_msin (wt+p)
snadno určíme fázový rozdíl těchto veličin:

okamžíté výchylky a rychlosti:	Dj = p/2
okamžité výchylky a zrychlení:	Dj = p
rychlosti a zrychlení:	Dj = p/2

Důležitý význam mají následující případy fázového rozdílu mezi dvěma veličinami harmonického pohybu stejné frekvence:

Dj=2kp, k=0,1,2,...	obě veličiny mají stejnou fázi
Dj=(2k+1)p, k=0,1,2,...	obě veličiny mají opačnou fázi

	Ve famulovském modelu můžete zadávat různé hodnoty počáteční fáze a porovnávat jednotlivé časové diagramy.
	Ověřte si své znalosti!