Řešení pohybové rovnice kmitavého pohybu.

Rovnici kmitavého pohybu x = xmsin (wt + j) lze odvodit srovnáním kmitavého pohybu s pohybem rovnoměrným po kružnici. Toto srovnání je správné, ale nekorektní - nelze zdůvodnit, zda tomu tak skutečně je. Z obrázku (případně experimentu) se zdá že ano, ale ve fyzice se nelze spoléhat pouze na to, co vidíme. Je třeba přesnější odvození. V dalším ukážeme jak dojít k rovnici harmonického kmitavého pohybu aniž bychom potřebovali kmitavý pohyb srovnávat s pohybem po kružnici. Vyjdeme ze znalosti síly, která na harmonicky kmitající těleso působí.

Mějme hmotný bod, který se pohybuje po přímce a na který působí síla F = - kx. Naším úkolem je zjistit, jak se tento bod pohybuje, tj. zjistit jeho polohu v závislosti na čase x = x(t). Sílu F = - kx dosadíme do druhého Newtonova zákona (F = ma) a získáme takzvanou pohybovou rovnici daného hmotného bodu.

(*)

Je to rovnice, jejímž řešením máme určit neznámou funkci x = x(t). Jelikož se v této rovnici kromě neznámé funkce x(t) vyskytují i její derivace (zde druhá derivace ), mluvíme o diferenciální rovnici. V matematice existují postupy, jak řešit takovéto diferenciální rovnice (tzn. jak najít všechny funkce, které této rovnici vyhovují). My si situaci zjednodušíme. Očekáváme, že řešením diferenciální rovnice (*) bude rovnice kmitavého pohybu x = xmsin (wt + j), kde . Stačí když ověříme, že tomu tak skutečně je. Nejprve vypočteme :


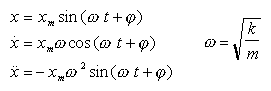
Nyní dosadíme do levé i pravé strany rovnice (*) a ověříme rovnost.


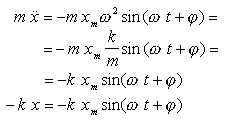
Levá strana se rovná pravé, x = xmsin (wt + j) je řešením diferencíální rovnice a hmotný bod na který působí síla F = - kx koná harmonické kmity.

Ukázali jsme, že jestliže na hmotný bod působí síla F = - kx, koná hmotný bod harmonické kmity a časovým diagramem je tedy graf funkce sinus. Možná jsme ještě někoho nepřesvědčili. Zkusme to tedy jinak, pomocí počítače a programu Famulus. Opět vyjdeme pouze ze znalosti síly F = - kx a pomocí základních vztahů pro rychlost a zrychlení se pokusíme získat výchylku. Popišme si tento model podrobněji: 

=============================================
              HARMONICKÉ KMITY
-----------------konstanty-------------------
dt=0.001
-------------počáteční hodnoty---------------
m=1       ! hmotnost kmitajícího tělesa
k=0.5     ! tuhost pružiny
t=0
x=5       ! počáteční hodnota souřadnice HB
v=0       ! počáteční rychlost HB
-------------------model---------------------
F=-k*x
a=F/m
v=v+a*dt
x=x+v*dt
t=t+dt
=============================================

Časový krok po kterém budeme v modelu postupovat označíme dt (=Dt) a zvolíme ho dostatečně malý. Na prvním řádku modelu vypočteme sílu, která na hmotný bod působí a podle 2. Newtonova zákona zrychlení HB v daném časovém okamžiku (druhý řádek). Pomocí zrychlení spočítáme rychlost HB. Víme že pro okamžité zrychlení přibližně platí
a změna rychlosti je
Jestliže k rychlosti v čase t přičteme tuto změnu, získáme velikost rychlosti v dalším časovém okamžiku t + Dt. Podobně jako třetí řadek získáme i čtvrtý.
Na pátém řádku se posuneme do dalšího časového okamžiku, Famulus vykreslí požadované hodnoty do grafu a výpočet se opakuje, ale již pro nový čas. Z počátečních hodnot (v = 0) je vidět, že kmitající těleso se v počátečním čase nachází v amplitudě výchylky (x = 5). Zbývá navolit zobrazení, například:
Po spuštění modelu získáme harmonický průběh výchylky. Nezbývá než konstatovat: jestliže na hmotný bod působí síla F = - kx, koná hmotný bod harmonické kmity a časovým diagramem je tedy graf funkce sinus.