4.3.2 Einsteinův-de Haasův pokus

V roce 1915 prováděli fyzikové Einstein a de Haas měření gyromagnetického poměru g vzorků různých látek (feromagnetika a paramagnetika). Přemagnetováním vzorku s magnetickým momentem docházelo současně ke změně momentu hybnosti vzorku , neboť oba momenty jsou vzájemně vázány vztahem

Shrňme nejdříve důležité výsledky experimentu.

Magnetický moment měly i vzorky látek, u jejichž atomů se předpokládal celkový magnetický moment rovný nule (nulový orbitální magnetický moment). Srovnej Sternův-Gerlachův experiment. Později byla tato skutečnost objasněna existencí vlastního magnetického momentu elektronu.

Pro některé látky, resp. jejich atomy, nabýval gyromagnetický moment odlišné hodnoty, než jaká vyplývá z klasické teorie (magnetický moment vznikající v důsledku pohybu nabité částice – elektronu, tzv. orbitální magnetický moment). Nejvyšší hodnota gyromagnetického poměru vycházela pro elektron ve slupkách s (nulové orbitální momenty)  a byla rovna dvojnásobku klasické hodnoty. Anomální hodnotu je možné objasnit až v rámci relativistické teorie, konkrétně její existence vyplývá z Diracovy rovnice pro elektron v magnetickém poli.

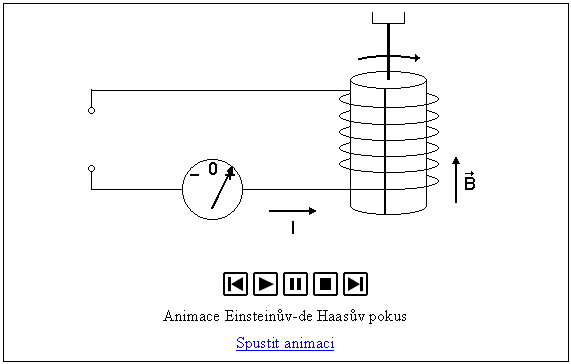
Uspořádání a princip experimentu

Váleček z feromagnetické nebo paramagnetické látky umístěný v cívce je zavěšen v podélné ose z na torzní niti. Pokud pustíme elektrický proud do indukční cívky, vzniklé magnetické pole () způsobí zmagnetování vzorku v jednom směru (magnetický moment ). Pokud poté provedeme komutaci elektrického proudu protékajícího cívkou, dojde k překlopení magnetické indukce a tím i k přemagnetování vzorku.

Změna magnetického momentu ve směru osy z pak souvisí s odpovídající změnou momentu hybnosti , kterou lze určit z úhlu pootočení vzorku na závěsu. V experimentu odpovídá kladné hodnotě záporná hodnota .

Gyromagnetický poměr pak lze určit jako , což je dáno skutečností, že platí , a analogicky též .

Pokud předpokládáme, že vzorek je tvořen N atomy daného prvku, můžeme oba momenty (moment hybnosti i magnetický moment) získat jako součet odpovídajících momentů jednotlivých atomů a výše uvedený gyromagnetický poměr vzorku je rovněž gyromagnetickým poměrem atomu, neboť

Zatímco v případě orbitálních momentů můžeme už i na základě klasické fyziky odvodit, pro gyromagnetický poměr , což je tzv. normální hodnota, v řadě případů lze naměřit hodnotu odlišnou.

Navíc se ukazuje, že k celkovému momentu, ať už se jedná o moment magnetický nebo moment hybnosti, přistupuje další dodatečný moment, který se podařilo interpretovat teprve na základě hypotézy o spinu elektronu.

V případě atomů s celkovým orbitálním momentem rovným nule pak dostáváme hodnotu , což se označuje jako anomální hodnota gyromagnetického poměru.

Nejjednodušší je interpretace tohoto gyromagnetického poměru v případě atomů, které mají jediný elektron ve valenční (pod)slupce, která je typu s (orbitální moment elektronu roven nule, např. stříbro, tj. Ag). V tomto případě totiž představuje gyromagnetický poměr pro vlastní (též spinové) momenty elektronu.

Pro elektron tedy platí

v případě orbitálních momentů , tj. normální hodnota

a v případě vlastních momentů , tj. anomální hodnota.

Zde jsou postupně z-ové komponenty orbitálního magnetického momentu, orbitálního momentu hybnosti, vlastního (resp. spinového) magnetického momentu a vlastního momentu hybnosti (spinu) elektronu.

Landého faktor

Protože v kvantové mechanice je výhodné uvádět momenty hybnosti v násobcích Planckovy konstanty a magnetické momenty elektronu nebo atomů v násobcích Bohrova magnetonu , můžeme pro gyromagnetické poměry elektronu psát , resp. , pro atomový gyromagnetický poměr pak obecně .

Bezrozměrový faktor g se označuje jako Landého faktor.

Pro orbitální (též dráhový) magnetický moment elektronu dostáváme vztahy pro velikost a z-ovou složku: , kde l je vedlejší kvantové číslo a m je magnetické kvantové číslo.

Pro vlastní (též spinový) magnetický moment elektronu dostáváme vztahy pro velikost a z-tovou složku: , kde s = 1/2 je spinové kvantové číslo a m_s = ±1/2 je magnetické spinové kvantové číslo. Tedy .

---

---