v bodě x = 0.
1.8 Komplexní funkce
Podobně jako vektorové funkce, bývají užitečné i funkce přiřazující argumentu komplexní číslo (reprezentované reálnou a imaginární složkou).
Teorii naleznete v kapitole 4.11 Multimediální encyklopedie nebo v kapitole 1.8 Breviáře
Příklad 1
Určete limitu komplexní funkce v bodě x = 0.
Řešení
Limitu komplexní funkce 
počítáme podle obecného vzorce 
.
(nejdříve si definujme funkce reprezentující reálnou a komplexní složku funkce)
(limitu reálné a komplexní složky spočteme pomocí funkce Limit)
Limitou je tedy komplexnní číslo 1+ 0 i = 1.
(V Mathematice lze přímo pracovat s komplexními čísly, imaginární jednotka, tj. 2. odmocnina z -1, je vkládána symbolem I, odmocina se počítá funkcí Sqrt).
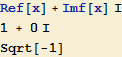
(Můžeme také definovat komplexní funkci )
(přímo na tuto komplexní funkci lze aplikovat funkci Limit)
Příklad 2
Určete derivaci komplexní funkce 
z předchozího příkladu obecně a v bodě x = 3.
Řešení
Postupujeme analogicky jako v případě prvního příkladu.
(nejdříve si definujme funkce reprezentující reálnou a komplexní složku funkce)
(derivaci reálné a komplexní složky spočteme pomocí funkce D)
Z těchto složek sestavíme příslušnou komplexní funkci odpovídající derivaci.
(Totéž obdržíme přímo zápisem komplexního výrazu)
(Mathematica však umožňuje funkci D pro derivování aplikovat i rovnou na komplexní funkci).
(Výsledek ale musíme upravit do obvyklého algebraického tvaru pomocí funkce ComplexExpand).
Dosazením hodnoty x = 3 do funkcí reálné a komplexní složky zjistíme hodnotu komplexní fce.
(v Matematice je možné přímo při výpočtu derivace určit její hodnotu v konkrétním bodě x = 3, a to pomocí symbolu /.)
(nebo pro obdržení hodnoty s desetinnou čárkou, v Mathematice reprezentované vždy tečkou, dosadíme trojku také s desetinnou čárkou, tedy tečkou).
Obdržíme tak komplexní číslo představující derivaci naší komplexní funkce v bodě x = 3.
