
1.4.1 Základní pojmy z teorie komplexních čísel
Komplexní čísla.
 Definice
Definice
Komplexní
čísla jsou uspořádané dvojice reálných čísel (označujeme
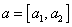
,
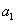
se nazývá
reálná
část,
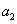
se nazývá
imaginární
část komplexního čísla
a), pro něž je definován vztah rovnosti
a operace sčítání a násobení takto (
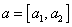
,
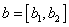
):
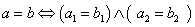
;
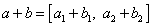
;
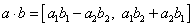
.
 Poznámka
Poznámka
a)
Dá se ukázat, že uvedené operace splňují komutativní, asociativní
a distributivní zákon, stejně jako u reálných čísel.
b)
Množinu všech komplexních čísel značíme 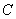 .
.
c)
Reálná část komplexního čísla
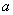
se často značí
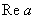
, imaginární část
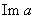
.
d)
Komplexní číslo
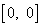
nazýváme (komplexní)
nulou a značíme prostě 0, stejně jako u reálných čísel.
 Definice
Definice
 Věta
Věta
Pro imaginární jednotku platí: 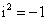 .
.
 Důkaz.
Důkaz.
Podle definice násobení reálných čísel dostáváme:
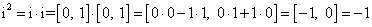
.
Cbd.
Gaussova
rovina.
Podobně jako reálná čísla lze geometricky znázornit přímkou,
lze komplexní čísla znázornit rovinou, zvanou Gaussova
rovina. V Gaussově rovině pak zavádíme
reálnou osu (vodorovnou), resp. imaginární
osu (svislou), na kterou nanášíme reálnou, resp. imaginární část komplexních
čísel. Z této představy je zřejmé, že komplexní čísla nelze seřadit podle
velikosti, tzn. není pro ně definována relace „a menší než b“
apod.
Rozdíl a podíl komplexních čísel.
Stejně jako u reálných čísel můžeme zavést rozdíl
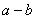
, resp. podíl
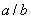
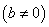
dvou komplexních
čísel jako jediné řešení rovnice
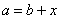
, resp.
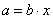
. Dostaneme toto
explicitní vyjádření:
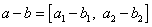
,
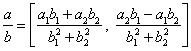
.
 Poznámka
Poznámka
Geometrický význam absolutní hodnoty: udává v Gaussově
rovině vzdálenost čísla a od čísla 0 (počátku souřadného systému).
 Definice
Definice
Čísla
a, pro která platí
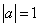
, nazýváme
komplexními
jednotkami.
b)
Imaginární jednotka patří mezi komplexní jednotky (protože
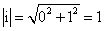
).
 Věta
Věta
Pro každá dvě komplexní čísla a, b platí:
![]() Definice
Definice ![]() .
.![]() přecházejí zavedené
operace sčítání a násobení v obyčejné sčítání a násobení prvních složek,
přičemž druhé složky jsou stále nulové. Proto komplexní čísla tvaru
přecházejí zavedené
operace sčítání a násobení v obyčejné sčítání a násobení prvních složek,
přičemž druhé složky jsou stále nulové. Proto komplexní čísla tvaru
![]() , tj. ta, která
mají imaginární část rovnu nule, můžeme ztotožnit s reálnými čísly.
Množina reálných čísel je tudíž podmnožinou množiny komplexních čísel, nebo,
řečeno jinak, pojem komplexního čísla je zobecněním pojmu reálného čísla.
, tj. ta, která
mají imaginární část rovnu nule, můžeme ztotožnit s reálnými čísly.
Množina reálných čísel je tudíž podmnožinou množiny komplexních čísel, nebo,
řečeno jinak, pojem komplexního čísla je zobecněním pojmu reálného čísla.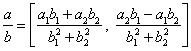 .
.