1.1 Mocnina a odmocnina v reálném oboru
Poznámka
Definici obecné mocniny reálného čísla s reálným exponentem je nutné připravit definicemi speciálnějších mocnin s přirozeným, celým a racionálním exponentem a definicí odmocniny. Je také nutné sledovat definiční obory jednotlivých operací, zejména to, zda je daná mocnina (odmocnina) definována i pro nulu, příp. záporný základ. Za každou definicí jsou uvedeny základní vlastnosti, které je bezpodmínečně nutné znát, protože na nich jsou založeny úpravy výrazů s mocninami a odmocninami.
Mocnina s přirozeným exponentem.
DefiniceNechť 
, 
. Pak 
-tou mocninou čísla
a je číslo 
, kde v naznačeném
součinu se a vyskytuje právě n-krát.
Věta
Pro každé , 
platí:
,
,
.
Mocnina s celým exponentem.
Definice
Nechť , 
. Je-li n=0,
pak pro 
definujeme
. Je-li
a , pak definujeme
. Symbol
je nyní definován
pro každé a každé celé n.
Věta
Pro každé 
, 
platí:
,
,
,
,
.
Odmocnina v reálném oboru.
Definice
Nechť , . Jestliže
, pak n-tou odmocninou
čísla a je takové kladné reálné číslo 
, pro které platí
. Toto číslo je
právě jedno a značí se 
. Místo 
se píše
. Pro 
se definuje
. Jestliže
a n liché,
pak se definuje 
.
Poznámka
Pro n sudé vždy platí 
, nikoli
, což platí pouze
pro 
.
Příklad
a) 
, nikoliv
.
b) 
.
c) Řešení rovnice 
v R vypadá
takto:
.
Věta
Pro každé 
, , 
platí:
,
,
,
,
.
Mocnina s racionálním exponentem.
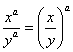Definice je reálné číslo,
r racionální číslo, které se dá (vždy) vyjádřit ve tvaru 
, kde p
je celé a q přirozené číslo. Pak definujeme 
. Speciálně
pro dostáváme
,
.
racionálních čísel
taková, že její limita je rovna a. Obecná mocnina 
se definuje jako
limita posloupnosti 
, tj. limita posloupnosti
mocnin s racionálním exponentem 
.
platí:
,
,
,
,
,
,
,
.