
1.2.2 Logaritmická funkce
 Definice
Definice
Logaritmickou funkcí (zkráceně logaritmem)
při základu a nazýváme funkci inverzní k funkci exponenciální.
Zapisujeme: 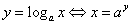 .
.
 Poznámka
Poznámka
a)
Nyní je jasné, proč jsme v definici exponenciály vyloučili případ 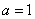 . Funkce
. Funkce
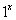 není prostá a
neexistuje k ní tedy funkce inverzní.
není prostá a
neexistuje k ní tedy funkce inverzní.
b)
Slovně řečeno: „logaritmem čísla x při základu a je
takové číslo y, pro které platí, že x se rovná a na y“.
c)
Ve dvou případech se zavádí speciální pojmenování a označení. Pro
základ 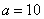 mluvíme o desítkovém
(dekadickém) logaritmu
a píšeme prostě
mluvíme o desítkovém
(dekadickém) logaritmu
a píšeme prostě 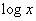 , tzn. vynecháváme
index 10. Pro základ
, tzn. vynecháváme
index 10. Pro základ 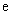 (Eulerovo
číslo) mluvíme o přirozeném logaritmu
(logaritmus naturalis) a píšeme
(Eulerovo
číslo) mluvíme o přirozeném logaritmu
(logaritmus naturalis) a píšeme 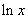 . V praxi
je významný také logaritmus o základu
. V praxi
je významný také logaritmus o základu 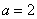 , který nazýváme
dvojkový (binární);
nemá zvláštní označení.
, který nazýváme
dvojkový (binární);
nemá zvláštní označení.
Graf logaritmické funkce.
Graf logaritmické funkce pro základ větší i menší
než jedna je na obrázku ( 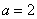 ). Také jeho tvar je nutné si
dokonale zapamatovat.
). Také jeho tvar je nutné si
dokonale zapamatovat.
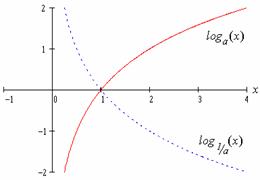
Základní vlastnosti logaritmické funkce.
 Věta
Věta
Logaritmická funkce je definována pouze pro kladná x, je prostá, pro
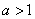 rostoucí, pro
rostoucí, pro
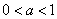 klesající, neomezená
zdola ani shora, graf prochází body [1, 0], [a, 1].
klesající, neomezená
zdola ani shora, graf prochází body [1, 0], [a, 1].
 Poznámka
Poznámka
Pozor! Obecně neplatí žádná obdobná věta o součinu, podílu nebo mocnině logaritmů,
tzn. že součin, podíl nebo mocninu logaritmů nemůžeme obecně nijak výhodně
upravit. Pouze podíl logaritmů o stejném základu se podle posledního vzorce
dá převést na jediný logaritmus o jiném základu, ale taková úprava nebývá
v praxi vhodná.
Logaritmování a odlogaritmování výrazu.
 Definice
Definice
Logaritmovat (méně přesně zlogaritmovat)
výraz znamená vyjádřit jeho logaritmus pomocí logaritmů jednodušších výrazů,
příp. proměnných. Používá se přitom zejména vět o logaritmu součinu, podílu
a mocniny.
 Řešená úloha
č. 1:
Řešená úloha
č. 1:
Logaritmujte při základu 10 výraz 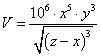 .
.
Řešení.
Aplikujeme operaci „log“ na obě strany rovnice a upravíme podle výše uvedených
vzorců:
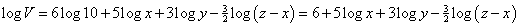 .
.
 Definice
Definice
Odlogaritmovat výraz znamená
vyjádřit výraz, jehož logaritmus je znám a je zapsán zpravidla pomocí logaritmů
jednodušších výrazů, příp. proměnných. Používá se opět vět o logaritmu součinu,
podílu a mocniny, tentokrát ale v obráceném směru.
 Řešená úloha č. 2:
Řešená úloha č. 2:
Odlogaritmujte výraz 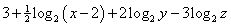 .
.
Řešení.
Naším úkolem je najít výraz 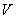 , aby platila
rovnice
, aby platila
rovnice
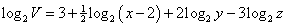 .
.
Můžeme použít dvě ekvivalentní metody.
Upravíme pravou stranu tak, aby měla tvar binárního logaritmu jediného výrazu:
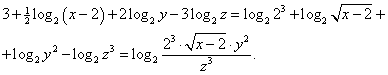
Nyní z rovnosti logaritmů plyne rovnost argumentů (logaritmus je funkce
prostá!), tzn.
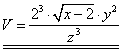 .
.
Jinou možností je aplikovat na každou stranu rovnice exponenciální funkci
se základem 2:
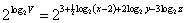 .
.
Tuto rovnici dále upravíme podle výše uvedených vět o logaritmické, resp.
exponenciální funkci:
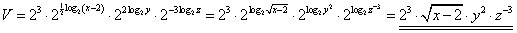 .
.
Druhý postup použijí asi ti studenti, kterým se lépe pracuje s exponenciální
funkcí než s funkcí logaritmickou.
![]() .
.![]() . Funkce
. Funkce
![]() není prostá a
neexistuje k ní tedy funkce inverzní.
není prostá a
neexistuje k ní tedy funkce inverzní.![]() mluvíme o desítkovém
(dekadickém) logaritmu
a píšeme prostě
mluvíme o desítkovém
(dekadickém) logaritmu
a píšeme prostě ![]() , tzn. vynecháváme
index 10. Pro základ
, tzn. vynecháváme
index 10. Pro základ ![]() (Eulerovo
číslo) mluvíme o přirozeném logaritmu
(logaritmus naturalis) a píšeme
(Eulerovo
číslo) mluvíme o přirozeném logaritmu
(logaritmus naturalis) a píšeme ![]() . V praxi
je významný také logaritmus o základu
. V praxi
je významný také logaritmus o základu ![]() , který nazýváme
dvojkový (binární);
nemá zvláštní označení.
, který nazýváme
dvojkový (binární);
nemá zvláštní označení.
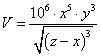 .
.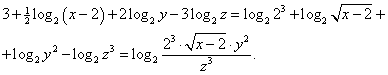
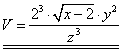 .
.