Argument komplexního čísla.
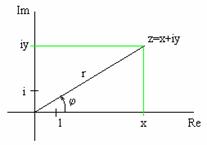
Na obrázku je znázorněno komplexní číslo ![]() v Gaussově rovině. Zavedeme polární souřadnice
v Gaussově rovině. Zavedeme polární souřadnice ![]() a
a ![]() vztahy
vztahy ![]() ,
, ![]() . Veličina
. Veličina
![]() má význam vzdálenosti
bodu
má význam vzdálenosti
bodu ![]() od počátku souřadnic
a
od počátku souřadnic
a ![]() představuje úhel
v radiánech, který svírá průvodič bodu
představuje úhel
v radiánech, který svírá průvodič bodu ![]() s kladným
směrem osy
s kladným
směrem osy ![]() .
.
Protože platí rovnice ![]() , můžeme veličinu
, můžeme veličinu
![]() ztotožnit s absolutní
hodnotou komplexního čísla
ztotožnit s absolutní
hodnotou komplexního čísla ![]() , tak jak byla
definována v kapitole 5.1.
, tak jak byla
definována v kapitole 5.1.
![]() Definice
Definice
Funkci, která komplexnímu číslu ![]() přiřazuje odpovídající
úhel
přiřazuje odpovídající
úhel ![]() , nazýváme argument
(řidčeji amplituda) komplexního čísla z a
značíme
, nazýváme argument
(řidčeji amplituda) komplexního čísla z a
značíme ![]() .
.
a)
Argument ![]() komplexního čísla
komplexního čísla
![]() je určen až na
libovolný násobek
je určen až na
libovolný násobek ![]() , hovoříme o tzv.
mnohoznačné funkci. I když tento termín obsahuje
určitý protimluv (funkce je standardně definována jako zobrazení, tzn. každému
vzoru přísluší maximálně jeden obraz), v teorii komplexní proměnné
je užitečný a běžně se používá (viz např. funkci komplexní odmocnina).
, hovoříme o tzv.
mnohoznačné funkci. I když tento termín obsahuje
určitý protimluv (funkce je standardně definována jako zobrazení, tzn. každému
vzoru přísluší maximálně jeden obraz), v teorii komplexní proměnné
je užitečný a běžně se používá (viz např. funkci komplexní odmocnina).
b)
Někdy se potřebujeme výše uvedené nejednoznačnosti vyhnout. Proto
definujeme tzv. hlavní hodnotu argumentu
komplexního čísla ![]() jako hodnotu z intervalu
jako hodnotu z intervalu
![]() (na střední škole
(na střední škole
![]() ) a značíme ji
velkým počátečním písmenem: Arg z.
) a značíme ji
velkým počátečním písmenem: Arg z.
Platí vztah ![]() .
.
Goniometrický tvar komplexního čísla.
![]() Definice
Definice
Zápis komplexního čísla z v podobě ![]() , kde
, kde
![]() ,
, ![]() , nazýváme
goniometrickým tvarem komplexního čísla
, nazýváme
goniometrickým tvarem komplexního čísla ![]() .
.
a)
Že je uvedený tvar možný, dokážeme snadno použitím vztahů
![]() a
a ![]() .
.
Přechod mezi algebraickým a goniometrickým tvarem.
Převod z goniometrického tvaru na algebraický je dán rovnicemi
![]() ,
, ![]() .
.
Převod z algebraického tvaru na goniometrický je trochu komplikovanější.
Absolutní hodnota problémy nedělá: ![]() .
.
Argument ![]() je dán řešením
některé z goniometrických rovnic
je dán řešením
některé z goniometrických rovnic ![]() ,
, ![]() ,
, ![]() , ale protože toto
řešení obecně není jednoznačné, je nutné ještě zvolit správný kvadrant,
např. pomocí znamének reálné a imaginární časti čísla z.
, ale protože toto
řešení obecně není jednoznačné, je nutné ještě zvolit správný kvadrant,
např. pomocí znamének reálné a imaginární časti čísla z.
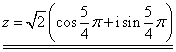 . Mohli bychom
použít i argument, který se od uvedeného liší o libovolný celočíselný násobek
. Mohli bychom
použít i argument, který se od uvedeného liší o libovolný celočíselný násobek
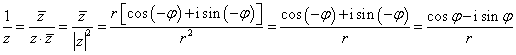 .
.