1.3.3 Goniometrické rovnice a nerovnice

Goniometrické rovnice.

Definice

Goniometrickou rovnicí nazýváme rovnici, obsahující funkce sinus, kosinus, tangens nebo kotangens (případně také sekans a kosekans) výrazu s neznámou.

Poznámka

Úplný výčet všech typů goniometrických rovnic není samozřejmě možný. Omezíme se proto pouze na základní typ. Složitější rovnice se řeší podle konkrétního tvaru, kde je to možné, převedením na základní typ, jinak numericky či graficky.

Definice
Kvadrantem rozumíme interval úhlů , kde . Např. první kvadrant je interval , druhý kvadrant , třetí kvadrant , čtvrtý kvadrant  atd.

Základní typy goniometrických rovnic.

Rovnice , resp. .

Na základě vlastností funkcí sinus, resp. kosinus je jasné že pro  nemají uvedené rovnice žádné řešení, tímto případem se dále nebudeme zabývat.

Metoda řešení.

Předpokládejme . První kořen  nalezneme snadno, aplikujeme-li na obě strany rovnice vhodnou cyklometrickou funkci: , resp. , odkud plyne , resp. . Nalezené kořeny jsou jedinými kořeny v oboru hodnot příslušných cyklometrických funkcí, tzn. , resp. .

Díky -periodicitě goniometrických funkcí sinus, resp. kosinus jsou právoplatnými kořeny všechna čísla , kde , tzn. kořenů je nekonečně mnoho.

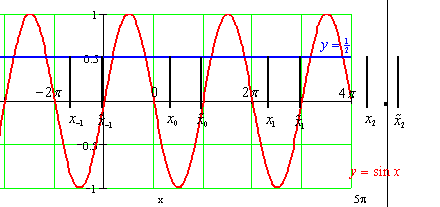
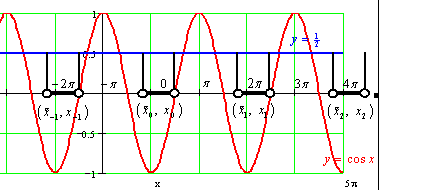
Pokud je , plyne z vlastností funkcí sinus a kosinus (viz např. graf), že v tomto případě existuje v některém kvadrantu sousedícím s kvadrantem kořene  další kořen , který generuje další nekonečnou množinu kořenů , kde . Konkrétní hodnotu kořene  určíme z vlastností goniometrických funkcí nebo přímo z grafu (viz také řešený příklad).

Množinově zapíšeme výsledné řešení pro případ  ve tvaru .

Rovnice tgx=a , resp. cotgx=a .

Na základě grafu funkcí tangens a kotangens je zřejmé, že uvedené rovnice mají řešení pro libovolné hodnoty čísla a na pravé straně.

Metoda řešení.

První kořen  nalezneme snadno, aplikujeme-li na obě strany rovnice vhodnou cyklometrickou funkci: , resp. , odkud plyne , resp. . Nalezené kořeny jsou jedinými kořeny v oboru hodnot příslušných cyklometrických funkcí, tzn. , resp. .

Díky -periodicitě goniometrických funkcí tangens, resp. kotangens jsou právoplatnými kořeny všechna čísla , kde , tzn. kořenů je nekonečně mnoho.

Množinově zapíšeme výsledné řešení ve tvaru .

Řešená úloha č. 1

Řešte v  rovnici .

Řešení.


Aplikujeme na obě strany rovnice funkci  a dostaneme první kořen . (hodnotu  bychom měli určit zpaměti, můžeme ji také vyčíst z tabulek nebo vypočítat pomocí kalkulátoru nebo počítače). Toto je ovšem řešení z oboru hodnot funkce , tzn. z intervalu .

Z grafu funkce  vidíme, že stejné hodnoty  jako v bodě  nabývá funkce  také ve druhém kvadrantu, a to v bodě  (jinak řečeno aplikujeme vztah ).

Uvážíme-li -periodičnost funkce , je výsledným řešením nekonečná množina izolovaných bodů .

Goniometrické nerovnice.

Poznámka

Podobně jako u rovnic se omezíme se pouze na základní typ goniometrických nerovnic.

Základní typy goniometrických nerovnic.

Nerovnice typu , , ,  
a nerovnice, které se od uvedených liší pouze znaménkem nerovnosti.

Metoda řešení.

K řešení používáme grafickou metodu. Hledáme takové intervaly proměnné , ve kterých graf goniometrické funkce leží nad („>”, „ “) nebo pod („<“, „ “) přímkou , přičemž u ostré nerovnosti vylučujeme průsečíky grafu a uvedené přímky z řešení, u neostré nerovnosti je naopak zahrnujeme do řešení. K určení uvedených průsečíků a tudíž také krajních bodů jednotlivých intervalů řešení je nutné řešit rovnici příslušnou k zadané nerovnici.

Nedílnou částí řešení goniometrické nerovnice je řešení příslušné goniometrické rovnice.

Řešená úloha č. 2

Řešte v  nerovnici .

Řešení.


Řešením rovnice  nalezneme kořeny  a , ležící ve dvou sousedních kvadrantech.

Z vlastností funkce kosinus je patrné, že v otevřeném intervalu  leží její graf nad přímkou , tudíž zde platí výchozí nerovnice a interval  patří do řešení. Vzhledem k -periodicitě funkce kosinus jsou řešením také intervaly posunuté vůči intervalu  o celočíselný násobek . Proto je celkovým řešením sjednocení nekonečného počtu otevřených intervalů .