1.3.1 Goniometrické funkceOblouková a stupňová míra.
Velikost rovinného úhlu se v praxi vyjadřuje ve stupních,
kdy přímému úhlu odpovídá hodnota 180º (a tedy pravému úhlu 90º,
plnému úhlu 360º). V teorii se dává přednost tzv. obloukové míře,
jejíž jednotkou je bezrozměrná jednotka zvaná radián. Je-li úhel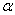 
v radiánech,
a úhel 
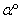tentýž úhel ve
stupních, pak platí převodní vztah
v radiánech,
a úhel tentýž úhel ve
stupních, pak platí převodní vztah 
.
Tudíž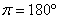 
, 
, 
, 
, 
, 
.
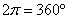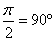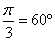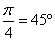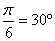, , , , , .Goniometrické funkce.
Poznámka
Goniometrické funkce jsou zavedeny buď pomocí jednotkové
kružnice nebo (pro ostré úhly) pomocí pravoúhlého trojúhelníka. Použijeme
druhý případ.
Definice
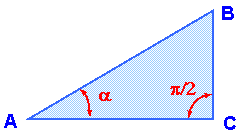
Nechť je dán pravoúhlý trojúhelník ABC s pravým úhlem u vrcholu C.
Úhel v obloukové míře u vrcholu A označíme . Čtyři základní
goniometrické funkce jsou pak definovány takto:
sinus: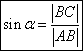 
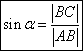, tzn. poměr velikostí
protilehlé odvěsny a přepony;
, tzn. poměr velikostí
protilehlé odvěsny a přepony;kosinus: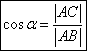 
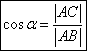, tzn. poměr velikostí
přilehlé odvěsny a přepony;
, tzn. poměr velikostí
přilehlé odvěsny a přepony;tangens: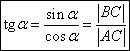 
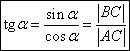, tzn. poměr velikostí
protilehlé odvěsny a přilehlé odvěsny;
, tzn. poměr velikostí
protilehlé odvěsny a přilehlé odvěsny;kotangens: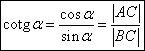 
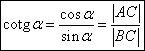, tzn. poměr velikostí
přilehlé odvěsny a protilehlé odvěsny.
, tzn. poměr velikostí
přilehlé odvěsny a protilehlé odvěsny.Poznámka
) a kosekans ( 
) se běžně
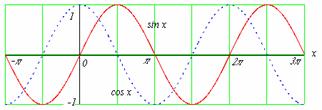
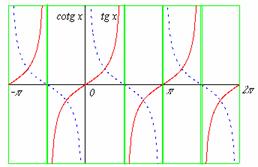
nepoužívají. Grafy goniometrických funkcí.
Velmi mnoho informací o goniometrických funkcích ukazují jejich grafy, které je
nutné znát zpaměti.
Základní vlastnosti goniometrických funkcí.
Věta
Funkce sinus, resp.
cosinus je 
- periodická,
spojitá, definiční obor
je
, obor
hodnot uzavřený interval
.
Funkce tangens,
resp. cotangens jsou 
- periodické,
definované v bez
množiny 
, resp.
, oborem
hodnot je celá
množina .
Žádná z uvedených funkcí není prostá.
Tabulka hodnot goniometrických funkcí
pro vybrané argumenty z prvního kvadrantu.
, 
.
.
, 
, 
, 
.
, 
.
, 
, 
.
, 
.
, 
,
, 
.
, 
, 
.