1.3.2 Cyklometrické funkce
Poznámka

Protože goniometrické funkce nejsou prosté v celém svém definičním oboru, neexistují k nim funkce inverzní. Omezíme-li se však pouze na část definičního oboru, ve které je daná goniometrická funkce prostá, můžeme k takto definované funkci přiřadit funkci inverzní, kterou pak nazýváme cyklometrickou funkcí. Používáme čtyři hlavní cyklometrické funkce.

Definice

Arkussinus.

Funkce (čteme „arkus sinus x“) je inverzní k  pro . Definičním oborem je uzavřený interval , oborem hodnot interval .

Arkuskosinus.

Funkce (čteme „arkus kosinus x“) je inverzní k  pro . Definičním oborem je uzavřený interval , oborem hodnot interval .

Arkustangens.

Funkce  (čteme „arkus tangens x“) je inverzní k  pro . Definičním oborem je celá množina , oborem hodnot interval .

Arkuskotangens.

Funkce   (čteme „arkus kotangens x“) je inverzní k  pro . Definičním oborem je celá množina , oborem hodnot interval .
Poznámka
a)      Cyklometrické funkce jsou nazývány také inverzními goniometrickými funkcemi, ale toto vyjádření není z výše uvedených důvodů zcela přesné.
b)      Výraz „ “ lze volně číst jako „úhel (doslova oblouk, lat. arcus), jehož sinus je “. Takových úhlů je ovšem obecně nekonečně mnoho, je míněn úhel z oboru hodnot příslušné cyklometrické funkce, v našem případě z intervalu . Obdobně pro další cyklometrické funkce.
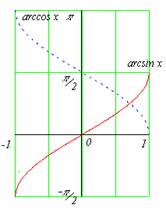
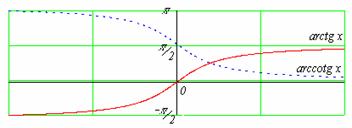
Grafy cyklometrických funkcí.

Většinu informací o definičním oboru, oboru hodnot a tvaru těchto funkcí lze jako obvykle získat z grafů, které je třeba znát zpaměti.

 
Poznámka
Všimněte si, že grafy cyklometrických funkcí jsou částmi grafů příslušných goniometrických funkcí, nakreslených do souřadného systému s přehozenými osami  a . Např. graf funkce  obdržíme tak, že do souřadného systému s přehozenými osami  a  nakreslíme graf funkce  (sinusovka bude tedy směřovat svisle nahoru), ze kterého ponecháme pouze část mezi hodnotami  a .
Vybrané vzorce pro práci cyklometrickými funkcemi.

Věta

Pro všechny úhly z definičního oboru platí následující vzorce:

Základní identity.
 pro ,  pro .
, , v obou případech pro .
 pro ,  pro ;
, , v obou případech pro .

Funkční hodnoty v opačném argumentu.

, ;

, ;

Z uvedených vzorců je zřejmé, že funkce arcsin a arctg jsou liché; funkce arccos a arccotg nejsou ani sudé ani liché, ale jejich průběh odpovídá liché funkci, posunuté ve funkčních hodnotách o .

Vztahy mezi cyklometrickými funkcemi.

Vztahy platí pro všechna , pro která jsou výrazy v rovnicích definovány:

, ;

, , .