1.4.2 Algebraický tvar komplexního čísla

---

Definice

Algebraickým tvarem komplexního čísla 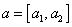 je vyjádření ve tvaru 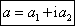, tzn. vyjádření ve tvaru součtu reálné části a 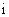-násobku imaginární části.

---

Poznámka

a)      Možnost uvedeného vyjádření plyne z dříve zavedených operací sčítání a násobení komplexních čísel a z definice imaginární jednotky: .

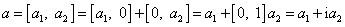b)      Algebraický tvar je výhodný z hlediska výpočetní jednoduchosti pro sčítání a odčítání komplexních čísel, dá se v něm také poměrně snadno násobit a dělit.

c)      Nejobvyklejší označení komplexní proměnné je písmenem „ 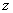“, v algebraickém tvaru nejčastěji 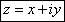, tohoto značení budeme i my přednostně používat.

---

Násobení a dělení v algebraickém tvaru.

V praxi je preferován algebraický tvar, který je daleko výhodnější než označení komplexních čísel jako uspořádaných dvojic reálných čísel. Je tomu tak proto, že v algebraickém tvaru můžeme sčítat, odčítat a násobit stejně jako v reálném oboru, pouze je třeba vzít na vědomí, že nesmíme míchat dohromady členy násobené 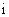 (ryze imaginární) a členy reálné, a že platí 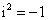. V algebraickém tvaru lze i dělit komplexní čísla, je ale třeba použít jistého „triku“, který nemá obdobu v reálné algebře.

---

Příklad č. 1

Násobení komplexních čísel v algebraickém tvaru:

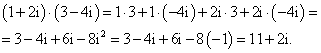
Postup je zřejmý. Roznásobíme závorky podle distributivního zákona, aplikujeme vztah  a nakonec sečteme zvlášť reálné a ryze imaginární členy.

---

Příklad č. 2

Dělení komplexních čísel v algebraickém tvaru:

.

Protože přímo dělit komplexním číslem neumíme, je prvním krokem rozšíření zlomku číslem komplexně sdruženým ke jmenovateli (tento důležitý „trik“ si zapamatujte!). Tím se ve jmenovateli objeví reálné číslo (druhá mocnina absolutní hodnoty původního jmenovatele), kterým již snadno dělíme čitatel tak, že vydělíme postupně jeho reálnou část a imaginární část.

---