Poznámka

Ke zjištění, zda je řada konvergentní čí nikoliv, slouží různá kritéria (nebo-li postačující podmínky). Uvedeme aspoň pro praxi nejdůležitější.

---

Věta (Leibnizova, pro alternující řady)

Nechť pro alternující řadu ,  platí , . Pak je tato řada konvergentní.

---

Věta (srovnávací kritérium)

Nechť řady  (1) a  (2) jsou řady s kladnými členy a nechť  pro skoro všechna  (tzn pro všechna  nejvýše s výjimkou konečného počtu). Řada (2) je tzv. majoranta k řadě (1). Pak z konvergence řady (2) plyne konvergence řady (1) a z divergence řady (1) plyne divergence řady (2).

---

Věta (odmocninné, Cauchyho kritérium)

Nechť je řada s kladnými členy a nechť . Pak je-li , je řada konvergentní, je-li , je řada divergentní.

---

Věta (podílové, d’Alembertovo kritérium)

Nechť je řada s kladnými členy a nechť . Pak je-li , je řada konvergentní, je-li , je řada divergentní.

---

Věta (Raabeovo kritérium)

 Nechť je řada s kladnými členy a nechť 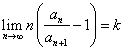. Pak je-li , je řada konvergentní, je-li , je řada divergentní.

---

Poznámka

Pokud v některém ze tří posledních kritériích nastane případ , nelze o konvergenci řady tímto kritériem rozhodnout.

---

Věta (Abelovo kritérium).

Jsou-li ,  dvě posloupnosti, z nichž  je ohraničená monotónní, pak konverguje-li řada , konverguje i řada .

---