2.3 Skalární součin a jeho aplikace

2.3.1 Skalární součin

Definice

Skalárním (vnitřním) součinem nazveme funkci, která dvojici vektorů  z V přiřazuje skalár označený  tak, že pro každé  z V a každý skalár k platí:

·         (aditivnost).
·         (homogenita).
·         (symetrie, komutativnost).
·         pro  (pozitivní definitnost).

Jednoduchým důsledkem uvedených axiomů je dále:

·        .
·        .
·        .

Poznámka

·        Tato definice platí přesně pouze pro vektorový prostor nad tělesem reálných čísel; v případě komplexních čísel nabývá třetí axiom tvaru a druhý důsledek tvaru  (pruh značí komplexní sdružení).

·        Dá se dokázat, že reálná funkce , definovaná na V, splňuje axiomy normy, tak jak byly uvedeny výše. Ukazuje se tedy, že je-li vektorový prostor vybaven skalárním součinem, je v něm možno takto zavést také normu (a tudíž i metriku). V dalším textu tento vztah mezi skalárním součinem, normou a metrikou předpokládáme.

Příklad

Typickým příkladem vektorového prostoru se skalárním součinem je 2- nebo 3-dimenzionální prostor geometrických, příp. fyzikálních vektorů, ve kterém je skalární součin vektorů  definován jako součin velikostí (norem) těchto vektorů a kosinu úhlu, který svírají: . Odtud se přejímá pro libovolné vektorové prostory pojem kolmosti vektorů.

2.3.2 Kolmost vektorů

Definice

Dva vektory  z V jsou na sebe kolmé (ortogonální) právě tehdy, je-li jejich skalární součin roven nule.

2.3.3 Ortogonální a ortonormální báze

Definice

Ortogonální bází vektorového prostoru V vybaveného skalárním součinem nazýváme takovou bázi, jejíž vektory jsou navzájem kolmé, tzn. jejich skalární součin je nulový. Mají-li navíc všechny vektory báze jednotkovou velikost (neboli jsou normovány k 1), mluvíme o ortonormální bázi.

Poznámka

Konkrétněji: je-li ortonormální bází, pak platí pro skalární součin libovolných dvou jejích prvků  vztah . Symbol na pravé straně, tzv. Kroneckerovo delta, je roven 1 pro i = j, jinak je roven 0.

Příklad

Nejpoužívanější ortonormální bází v prostoru  je báze tvořená vektory , , . Důkaz její ortonormality přenecháváme čtenáři.

2.3.4 Skalární součin v ortonormální bázi

Věta

Nechť je dán vektorový prostor V se skalárním součinem, jeho ortonormální báze  a dva vektory  z V, které lze vyjádřit ve tvaru , . Pak pro skalární součin těchto vektorů platí

,

což je známý tvar výpočtu skalárního součinu jako součtu součinů jednotlivých souřadnic.

Důkaz

Důkaz je snadný: .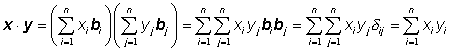

2.3.5 Průmět a projekce vektoru

Definice

Průmětem vektoru  do vektoru  nazýváme vektor , kde  je jednotkový vektor ve směru vektoru . Číslo  nazýváme projekcí vektoru do vektoru .

Poznámka

V případě geometrických nebo fyzikálních vektorů v 2 a 3dimenzionálním prostoru se dá projekce vektoru  do vektoru  vyjádřit ve tvaru  (gama je úhel mezi vektory , ), ze kterého je zřejmý původ zavedené terminologie.

Věta

Souřadnice vektoru v libovolné ortonormální bázi je totožná s projekcí tohoto vektoru do příslušného bázového vektoru.

Důkaz

Vypočtěme projekci vektoru  do vektoru báze :

,

neboť pro vektory báze platí relace ortonormality .