2.5 Matice – základní definice

---

2.5.1 Definice matice

Definice

Maticí  typu (m, n) nazýváme schéma  čísel (reálných nebo i komplexních) sestavených do m řádků n sloupců

.

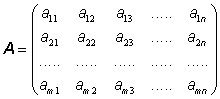Často používaný zkrácený zápis (pokud víme, o jaký typ matice se jedná) je . Je-li , pak se  nazývá čtvercovou maticí m-tého stupně (m-tého řádu), jinak hovoříme o matici obdélníkové.

---

Definice

Prvky , pro daný index i tvoří i-tý řádek, prvky , pro daný index k tvoří k-tý sloupec. První index v označení prvku  nazýváme řádkovým, druhý sloupcovým. Řádky a sloupce se souhrnně nazývají řady matice .

---

Definice

Prvky  tvoří hlavní diagonálu a nazývají se hlavní prvky, prvky  tvoří vedlejší diagonálu.

---

Definice (rovnost matic)

Matice  se rovná matici  právě tehdy, jsou-li obě matice stejného typu a jejich stejnolehlé prvky se rovnají. Matematicky zapsáno:.

---

2.5.2 Stopa matice

Definice

Stopou čtvercové matice  řádu n nazýváme součet jejích hlavních prvků:

.

---

Poznámka

Označení „Tr“ pochází z anglického „trace“, označení „Sp“ z německého „Spur“.

---

2.5.3 Speciální matice

Definice

·        Nulovou maticí nazýváme matici, jejíž všechny prvky se rovnají nule. Značíme obvykle symbolem  nebo i číslem 0.

·        Diagonální maticí nazýváme čtvercovou matici, u které prvky na hlavní diagonále jsou různé od nuly a všechny ostatní prvky rovny nule.

·        Jednotkovou maticí nazýváme takovou diagonální matici, jejíž všechny hlavní prvky jsou rovny 1. Jednotková matice se obvykle značí ,  nebo i číslem 1.

·        Horní (pravou) trojúhelníkovou maticí nazýváme čtvercovou matici , jestliže pod hlavní diagonálou jsou všechny prvky nulové, tzn. .

·        Dolní (levou) trojúhelníkovou maticí nazýváme čtvercovou matici , jestliže nad hlavní diagonálou jsou všechny prvky nulové, tzn. .

---