2.11 Vlastní čísla a vektory matic 
Definice (vlastní čísla a vektory matice)
Nechť je dána čtvercová matice 
řádu n
a nenulový vektor (sloupcová matice) 
typu 
. Platí-li
,
tzn. vynásobení vektoru 
zleva maticí 
je ekvivalentní
vynásobení vektoru 
určitým číslem
, nazýváme vektor
vlastním
(charakteristickým) vektorem
matice 
a číslo 
příslušným vlastním
(charakteristickým) číslem
matice 
.
Definice
Charakteristickou maticí čtvercové
matice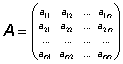 
nazýváme matici
,
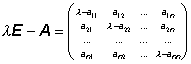kde veličina 
je reálná nebo
komplexní proměnná.
Poznámka
Charakteristická matice je zřejmě funkcí proměnné 
.
Definice
Polynom 
n-tého
řádu v proměnné 
, tj. determinant
charakteristické matice k matici 
, nazýváme charakteristickým
polynomem.
Věta
Vlastními čísly matice 
jsou kořeny 
charakteristického
polynomu 
.
Poznámka
Věta dává jasný návod, jak nalézt vlastní čísla matice. Pokud je však charakteristický polynom stupně vyššího než třetího, nemusí být nalezení jeho kořenů jednoduchou úlohou.
Věta
Vlastní čísla trojúhelníkové matice jsou rovna prvkům v hlavní diagonále (hlavním prvkům).
Důkaz
Důkaz je snadný, stačí si připomenout, že determinant trojúhelníkové matice je roven součinu jejích hlavních prvků.
Poznámka
Nalezení vlastních čísel trojúhelníkové (případně diagonální) matice je zjevně triviální úlohou.
Definice
(podobnost matic)
Čtvercové matice 
, 
téhož řádu nazýváme
podobnými, existuje-li taková matice 
, že platí 
. Hovoříme o tzv.
podobnostní transformaci.
Věta
Podobné matice mají stejný charakteristický mnohočlen, stejná vlastní čísla a stejnou stopu.
Poznámka
Dvě poslední věty nabízejí další možnost výpočtu vlastních
čísel - totiž provedením takové podobnostní transformace, která danou matici
převede na matici trojúhelníkovou. Ovšem nalezení vhodné transformační matice
není nic snadného,
v praxi se k tomu používají složité numerické algoritmy.
Definice
·
Hermitovskou
(hermitovsky symetrickou) maticí
nazýváme matici, pro niž 
,
neboli 
(pruh
značí komplexní sdružení, horní index + tzv.
hermitovské sdružení, tzn. současnou transpozici
matice a její komplexní sdružení).
·
Ortogonální
maticí rozumíme matici, pro kterou platí 
.
·
Unitární
maticí rozumíme matici, pro kterou platí 
.
Poznámka
S uvedenými typy matic se velmi často setkáváme v praxii. Níže uvádíme jejich vybrané vlastnosti, které mají vztah k problematice vlastních čísel.
Věta
·
Vlastní čísla
hermitovské matice jsou reálná.
·
Vlastní čísla
reálné symetrické matice jsou reálná.
·
Modul (absolutní
hodnota) každého vlastního čísla unitární matice je roven jedné.
·
Vlastní vektory
hermitovské matice příslušné různým vlastním číslům jsou navzájem ortogonální.
·
Vlastní vektory
unitární matice, příslušné různým vlastním číslům, jsou navzájem ortogonální.
·
Nechť 
je hermitovská
matice. Pak existuje unitární matice 
taková, že matice
je diagonální
(a reálná).
·
Nechť 
je reálná symetrická
matice. Pak existuje reálná ortogonální matice 
taková, že matice
je diagonální
(a samozřejmě také reálná).