2.10 Řešení soustav lineárních rovnic maticovým
počtem 
Definice
Nechť je dána soustava m lineárních rovnic o n neznámých:
.
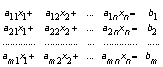Pak matici
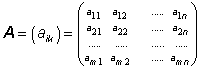
typu 
nazýváme
maticí soustavy.
Matici
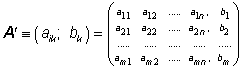
typu 
nazýváme
rozšířenou maticí soustavy.
Sloupcovou matici
,
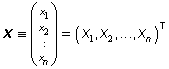resp.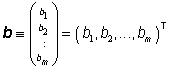 
,
nazýváme vektorem (sloupcem) neznámých, resp. vektorem (sloupcem) pravých stran.
Věta
(maticový zápis soustavy lineárních rovnic)
Soustavu
m lineárních rovnic o n neznámých můžeme zapsat v maticovém
tvaru 
.
Věta (Frobeniova)
Soustava
lineárních rovnic je řešitelná právě tehdy,
má-li matice soustavy 
a
rozšířená matice soustavy 
stejnou
hodnost h. Pak pro 
existuje
právě jedno řešení, pro 
existuje
řešení nekonečně mnoho.
Poznámka
·
Uvážíme-li
platnost relace 
,
platí v případě, kdy soustava má řešení, tj. kdy 
,
nerovnost 
.
Jestliže je tato nerovnost v konkrétním případě ostrá, tj. 
,
znamená to, že soustava obsahuje pouze 
signifikantních
rovnic a zbytek (
)
jsou rovnice, které z těchto rovnic vyplývají a můžeme je jako nadbytečné
vypustit.
·
Případ,
kdy soustava nemá žádné řešení, tj. kdy 
,
nastává právě tehdy, když se v soustavě vyskytuje aspoň jedna rovnice,
která je nekompatibilní s ostatními (rovnice se navzájem vylučují).
Věta
Homogenní
soustava rovnic lineárních rovnic, tj. soustava, jejíž vektor pravých
stran 
je
nulovým vektorem, má vždy aspoň jedno řešení.
Důkaz
Důkaz plyne z Frobeniovy věty, neboť u homogenní soustavy se matice rozšířená se od matice soustavy liší pouze přidáním nulového sloupce a tato operace nemění hodnost matice.
Věta (Cramerovo
pravidlo)
Jestliže
determinant matice soustavy n lineárních rovnic o n neznámých
je různý od nuly (tj.
nebo-li matice soustavy je regulární), pak má soustava právě jedno řešení
,
kde
a 
je
determinant matice, která vznikne z matice soustavy 
tak,
že v ní i-tý sloupec nahradíme vektorem pravých stran 
.
Poznámka
Cramerovo pravidlo nemá velký význam pro praxi, protože počítání determinantů je většinou pracné. Jeho výhodou snad je pouze možnost čistě mechanického výpočtu. Důležitější je význam teoretický. Cramerovo pravidlo totiž formuluje obecný vzorec pro analytické vyjádření jednotlivých kořenů soustavy lineárních rovnic (s regulární maticí soustavy).