2.9 Inverzní matice 
Definice
Inverzní maticí k čtvercové
matici 
nazýváme
(pokud existuje) takovou matici 
stejného
typu, pro kterou platí 
,
kde 
je
jednotková matice.
Věta
Následující výroky jsou ekvivalentní:
·
Inverzní
matice k matici 
řádu
n existuje.
·
Hodnost
matice 
je
rovna jejímu řádu, tj. 
.
·
Determinant
matice 
je
různý od nuly.
Poznámka
Vidíme,
že regulární matici můžeme definovat třemi způsoby: 
.
Věta (vlastnosti inverzní
matice)
Pro inverzní matici platí:
,
,
.
Důkaz
Důkaz např. druhého vzorce je velmi snadný:
.
Věta (výpočet inverzní
matice pomocí adjungované matice)
Inverzní
matici k regulární matici 
řádu
n lze vyjádřit ve tvaru
,
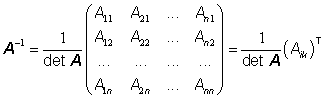kde 
je
algebraický doplněk prvku 
.
Definice
Matici
,
tj. transponované matici algebraických doplňků, říkáme matice
adjungovaná.
Poznámka
(Gaussova metoda inverze matic)
K určení
inverzní matice se kromě uvedeného výpočtu pomocí adjungované matice používá
(zejména pro vyšší řády) tzv. Gaussovy metody inverze
matic. Tato metoda je založena na tom, že k inverzní matici 
lze
přejít pomocí pouze řádkových (nebo pouze sloupcových) elementárních úprav
matice 
,
přičemž nejprve se snažíme dostat jednotkovou matici 
a
pak aplikací týchž elementárních úprav ve stejném pořadí přejdeme od matice
k inverzní
matici 
.
V praxi vždy vystačíme se třemi operacemi: přičtením lineární kombinace
řádků k jinému řádku, vynásobením řádku číslem různým od nuly a přehozením
pořadí řádků. Pokud není možno uvedeným postupem obdržet matici 
,
je matice 
singulární.
Příklad
Invertujme matici druhého řádu 
.
Nejprve pomocí adjungované
matice: Matice algebraických doplňků je 
, po transpozici
, dále snadno spočítáme
. Tudíž 
.
Nyní Gaussovou metodou: Matici 
a jednotkovou
matici 
si napíšeme buď
vedle sebe nebo do tzv. blokové matice (matice, rozdělené čarami na bloky)
a provádíme elementární úpravy současně na obou maticích:
.
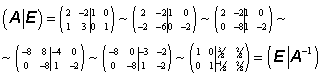Výsledky získané oběma metodami jsou pochopitelně stejné.
Definice (celočíselná
mocnina matice)
Pro čtvercovou
regulární matici 
definujeme
celočíselnou mocninu takto (
):
·
,
tzn. jako opakované násobení n stejných matic.
·
,
tzn. jako opakované násobení n inverzních matic .
·
.
Věta
Obdobně
jako pro číselné mocniny platí:
,
.
Poznámka
Přirozenou mocninu matice jsme ovšem mohli definovat již po definici maticového násobení, teprve nyní, tj. po definici inverzní matice, však můžeme definovat i mocninu se záporným exponentem.