2.8 Determinant matice
Definice
Determinantem čtvercové
matice 
řádu
n nazýváme číslo 
,
kde sčítáme přes všechny permutace P množiny 
.
Veličina 
je
tzv. znaménko permutace P.
Poznámka
·
Znaménko
permutace P je dáno vztahem 
,
kde r je počet tzv. inverzí v permutaci
P. Inverzí v permutaci 
nazýváme
každou dvojici 
,
pro kterou platí 
.
Pokud je číslo r sudé, hovoříme o sudé permutaci
a její znaménko je rovno 1, pokud je r liché, jedná se o lichou
permutaci a její znaménko je rovno –1. Např. permutace 
je
lichá, protože obsahuje 3 inverze: 
.
·
Kromě
uvedeného značení pomocí symbolu „
“
se v praxi často používá také řeckého písmene 
(většinou
s nějakým rozlišujícím indexem, např. 
nebo
apod.).
Jinou možností je zápis analogický zápisu matice, kdy kulaté závorky nahrazují
svislé čáry jako u absolutní hodnoty. Např. symbol 
označuje
determinant matice 
.
·
Sčítance
se
nazývají členy determinantu. Z definice
determinantu je zřejmé, že každý člen determinantu 
obsahuje
součin n prvků matice 
,
přičemž z každého řádku a sloupce matice 
je
vybrán právě jeden prvek.
Definice
Matice, jejíž determinant je různý od nuly, se nazývá regulární. V opačném případě hovoříme o matici singulární.
Definice
Subdeterminantem
(minorem) k-tého řádu matice 
typu 
nazýváme
determinant matice, která vznikne z matice 
vypuštěním tolika
řádků a sloupců, aby z ní zbyla čtvercová matice k-tého řádu.
Věta (výpočet
determinantů prvního řádu)
Pro matici
prvního řádu 
platí:
.
Poznámka
·
Determinantem
matice prvního řádu je tedy hodnota jediného jejího prvku.
·
Není zde vhodný zápis determinantu pomocí svislých čar, neboť ten by sváděl
k mylnému dojmu, že se jedná o absolutní hodnotu prvku.
Věta
(výpočet determinantů druhého řádu)
Determinant
matice druhého řádu lze počítat podle vzorce 
.
Poznámka
Jedná se o definiční vztah, aplikovaný na případ matice druhého řádu, čili nic nového. Uvedený vzorec se ale velmi snadno pamatuje (násobí se „do kříže“).
Věta
(výpočet determinantů třetího řádu)
Pro výpočet
determinantu matice třetího řádu se používá schéma zvané Sarrusovo
pravidlo: K matici 
připíšeme
první dva sloupce (obdobně je možné formulovat toto pravidlo pro řádky) a
pak provádíme součiny po přímých čárách tak, jak je naznačeno na obrázku,
přičemž ve směru zleva doprava je znaménko kladné, ve směru zprava doleva
záporné.
Poznámka
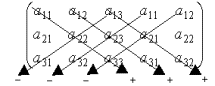
Také zde se nejedná o nic nového oproti definici, uvedené schéma nám pouze usnadňuje nalezení jednotlivých členů determinantu včetně znamének.
Výpočet determinantů matic řádu vyššího než třetího není vhodné provádět přímo podle definice (ani v počítačových programech), protože počet členů je příliš velký a výpočetní čas rychle roste s řádem matice. Proto se používá jiných metod, založených na vybraných vlastnostech determinantů.
Věta (vlastnosti determinantů)
·
.
·
.
·
(pro
čtvercové matice téhož řádu).
·
Zaměníme-li
v matici navzájem dva řádky nebo dva sloupce, změní determinant znaménko.
·
Společného
nenulového činitele jednoho řádku nebo sloupce lze vytknout před determinant.
·
Determinant
je roven nule právě tehdy, jestliže prvky alespoň jednoho řádku (sloupce)
jsou rovny nule nebo jestliže nějaký řádek (sloupec) je lineární kombinací
ostatních řádků (sloupců).
·
Determinant
se nezmění, přičteme-li k libovolnému řádku (sloupci) jakoukoliv lineární
kombinaci ostatních řadků (sloupců).
Definice
Algebraickým doplňkem prvku 
matice
nazýváme
číslo 
,
kde 
je
subdeterminant (minor) vzniklý z matice 
vynecháním
i-tého řádku a k-tého sloupce.
Věta (rozvoj
determinantu podle prvků vybrané řady)
Rozvoj
determinantu podle i-tého řádku:
.
Rozvoj
determinantu podle k-tého sloupce:
.
Symbol
ve
vzorcích výše označuje algebraický doplněk prvku 
.
Poznámka
· Věta převádí výpočet determinantu n-tého řádu na výpočet n determinantů (n-1)-ho řádu. Počet členů determinantu a jeho výpočetní náročnost se tím obecně nemění. V praxi je však výhodné počítat determinant rozvojem podle prvků té řady, která obsahuje nejvíce nulových prvků. Pak se totiž nemusí počítat příslušné determinanty nižšího řádu a to vede k významnému urychlení výpočtu.
· Před vlastním výpočtem determinantu je kromě výběru vhodné řady dále možné v této řadě vynulovat co nejvíce prvků použitím úprav, které nemění hodnotu determinantu (viz výše). „Maximálním programem“ je převést matici na trojúhelníkovou, tzn. vynulovat všechny prvky pod nebo nad hlavní diagonálou.
Věta
Determinant trojúhelníkové (horní nebo dolní) matice je roven součinu jejích hlavních prvků.
Důkaz
Uvažujme
např. dolní trojúhelníkovou matici 
řádu
n. V prvním řádku této matice může být pouze jediný nenulový prvek,
diagonální prvek 
.
Rozvoj jejího determinantu podle prvního řádku má tedy pouze jeden člen: 
.
Algebraický doplněk 
je
roven determinantu matice vzniklé z matice 
odstraněním
prvního řádku a prvního sloupce. Tato matice je řádu o jedna menšího a je
rovněž dolní trojúhelníková. Můžeme tudíž provést analogický rozvoj jejího
determinantu podle prvního řádku. Opakováním provedených úvah dojdeme až k jednoprvkové
matici 
, jejíž
determinant je roven jejímu jedinému prvku, a odtud k závěrečnému vyjádření
.