12.2 Plošný integrál prvního druhu

Definice

Budiž    jednoduchá hladká plocha a   spojitá funkce definovaná na nějakém okolí každého bodu  .  Pak předpisem

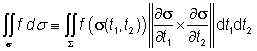
definujeme plošný integrál prvního druhu funkce  f  na ploše  s. [1]  V případě uzavřené plochy se obvykle používá symbol  .

Poznámka

Pro malé změny parametrů  dt₁  či  dt₂  můžeme popsat změny souřadnic bodů ležících na dané ploše v okolí vybraného bodu  pomocí věty o totálním diferenciálu (viz kap. 2.4 ):

·        mění-li se  t₁  a  t₂  zůstává konstantní, lze psát  ,
·        pokud se mění  t₂  a naopak   t₁  zůstává konstantní, platí .

Podle toho se tedy obdélník o stranách  dt₁  a  dt₂  (patřící do množiny  S zobrazí na element plochy  s,  který odpovídá v prvním přiblížení kosodélníku o stranách    a  .  Podle elementárního vzorce je plošný obsah tohoto kosodélníka dán velikostí vektorového součinu .  Proto (porovnáme-li formálně pravou a levou stranu definičního vztahu pro plošný integrál prvního druhu)

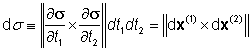
odpovídá s přesností do prvního řádu plošnému obsahu infinitezimální části plochy  s vymezené hodnotami parametrů t₁ a t₂ z dvojrozměrného intervalu  .

Poznámka

Z definice plošného integrálu prvního druhu a z předcházející poznámky vyplývá, že  je roven plošnému obsahu plochy  s. [2]

Věta (nezávislost plošného integrálu prvního druhu na parametrizaci)

Nechť   a    jsou dvě jednoduché hladké plochy takové, že

·        ,
·        existuje vzájemně jednoznačné spojitě diferencovatelné zobrazení    splňující .

Pak pro libovolnou spojitou funkci   definovanou na nějakém okolí geometrického obrazu    platí

.

Hodnota plošného integrálu prvního druhu nezávisí tedy na parametrizaci plochy.