12.1.1 Tečná rovina, normálový vektor

Poznámka

Budiž    nějaký bod zadané plochy  s.  Na okolí tohoto bodu je možno zobrazení  s  aproximovat pomocí věty o prvním diferenciálu [1]

,

kde i = 1, 2, 3. Snadno zjistíme, že uvedená rovnice, v níž přibližnou rovnost nahradíme rovností přesnou, odpovídá parametrickému zadání roviny, a to podle geometrické interpretace prvního diferenciálu roviny tečné k ploše  s  v bodě  x⁽⁰⁾. Vektory

 ,

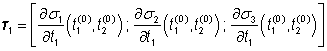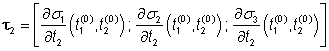
jsou tedy tečnými vektory k ploše  s  v bodě  x⁽⁰⁾. Jak je vidět z přímého porovnání, odpovídají složky obou vektorů sloupcům Jacobiho matice  s  počítaným v bodě  x⁽⁰⁾.  Podle předpokladu jsou tedy lineárně nezávislé a skutečně zadávají rovinu.

Výše uvedený výpočet můžeme ovšem provést jen tehdy, je-li možno aplikovat větu o prvním diferenciálu - jsou-li například splněny předpoklady definice jednoduché plochy. Existují ovšem obecnější plochy, které nemají v každém bodě tečnou rovinu. Těmi se zde ale zabývat nebudeme.

Definice

Nenulový vektor vázaný v zadaném bodě    plochy  s  a kolmý k tečné rovině k této ploše (viz předcházející poznámka), nazveme vektorem normálovým  k ploše  s  v bodě  .   Má-li tento vektor jednotkovou délku (eukleidovskou normu), nazveme jej jednotkovým normálovým vektorem. Obvykle jej budeme označovat písmenem  n. [2]

Poznámka

Normálových vektorů existuje ve skutečnosti nekonečně mnoho – zaplňují jednorozměrný vektorový prostor. Dokonce ani jednotkový normálový vektor není určen jednoznačně – existují vždy dva, které se navzájem liší znaménkem. Ze všech možných normálových vektorů k zadané ploše v zadaném bodě stačí ale znát jen jeden vybraný. Snadno pak umíme zkonstruovat i všechny ostatní. Tímto vybraným normálovým vektorem může být například vektorový součin dvou libovolně zvolených lineárně nezávislých tečných vektorů.

Poznámka

Velmi jednoduše se hledá normálový vektor pro plochu zadanou implicitně. Nechť    je libovolný vektor ležící v rovině tečné k ploše    v bodě  x⁽⁰⁾.  Pak můžeme pro v absolutní hodnotě malé číslo  a  přibližně psát [3]

.

Bod  x⁽⁰⁾  je ale bodem plochy, musí tedy platit  .  V limitě    přecházejí přibližné rovnosti na přesné a platí tedy

.

Vzhledem k tomu,že  t  je libovolný vektor z roviny tečné v zadaném bodě k zadané ploše a gradient  F  podle předpokladu nenulový, je nutně     jedním z hledaných normálových vektorů.

Definice

Nechť geometrický obraz plochy  s  je hranicí nějaké oblasti  .  Pak plochu  s  nazveme uzavřenou. Normálový vektor, který míří ven z oblasti  V,  nazýváme vnějším normálovým vektorem nebo také vektorem vnější normály.

Příklad

Pojmy zavedené výše můžeme názorně ilustrovat na příkladu kulové plochy.