12.1 Plochy

V této kapitole se budeme zabývat dvojrozměrnými plochami v . Až na několik málo výjimek by bylo možno vše uvedené zobecnit i na (n-1)-rozměrné nadplochy v , výklad by se ovšem patřičně komplikoval. Omezíme se proto na z hlediska aplikací pravděpodobně nejvýznamnější případ ploch v trojrozměrném prostoru.

Definice

Nechť   je jednou spojitě diferencovatelné zobrazení oblasti   do  .  Matici

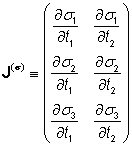
nazveme Jacobiho maticí zobrazení  s.

Jsou-li sloupce této matice v každém bodě množiny  S  lineárně nezávislými vektory a zobrazení  s je prosté (a inverzní zobrazení je navíc  s^-1  spojité), nazveme  s jednoduchou hladkou plochou. [1] Obraz množiny  S  v tomto zobrazení nazveme geometrickým obrazem plochy  s  a budeme jej označovat  .

Poznámka

Podle výše uvedené definice popisujeme jednotlivé body plochy  s  pomocí dvou reálných parametrů  t1  a  t2.  Hovoříme proto o parametrickém zadání plochy. [2]  Obecnou plochu v    můžeme zadat ovšem i jinými způsoby. Uveďme si dva nejdůležitější z nich.

Explicitní zadání plochy
Odpovídá-li geometrický obraz plochy grafu nějaké spojitě diferencovatelné funkce  ,  je možno tuto plochu popsat právě touto funkcí. Hovoříme pak o explicitním zadání plochy. Podle potřeby můžeme použít i funkcí    nebo  . Přejít od explicitního zadání plochy k zadání parametrickému není obtížné [3]:

,  ,  a  .

Implicitní zadání plochy
Plochu je dále možno popsat prostřednictvím vazebné podmínky, kterou musí splňovat souřadnice bodů na ní ležících [4]. Nechť  je nenulová spojitě diferencovatelná funkce tří reálných proměnných, která nemá v žádném bodě nulový gradient. Pak je možno tuto vazebnou podmínku zapsat ve tvaru

.

O takovém zadání plochy hovoříme jako o zadání implicitním. Alespoň lokálně od něj můžeme přejít k zadání explicitnímu tak, že rovnici  vyřešíme vzhledem k některé proměnné, např. z.

Příklad

Jako příklad hladké plochy můžeme uvést plochu kulovou.