7.4 Trojné a trojnásobné integrály na trojrozměrných intervalech

Definice

Pod uzavřeným intervalem z  rozumíme kartézský součin  .

Definice

Nechť    je uzavřený interval z    a  ,    a    jsou dělení intervalů  ,   a   .  Pak množinu

nazveme dělením intervalu  I  a číslo

normou dělení  D.

Definice

Nechť    je dělení uzavřeného intervalu  I  z   a    množina uspořádaných trojic reálných čísel takových, že  ,    a  .  Dále nechť je  f  omezená funkce na intervalu  I [1]. Pak součet

nazveme Riemannovou integrální sumou funkce  f  pro dělení  D  a  množinu čísel  z.

Definice

Nechť    je posloupnost dělení intervalu  I,  jejichž norma konverguje k nule, ,  a  zN  posloupnost množin trojic čísel   z předcházející definice přiřazených dělením  . Funkce    nechť je definována a omezená na intervalu  I.  Existuje-li pro všechny takové posloupnosti jejich společná limita [2]

,

nazveme tuto limitu trojným Riemannovým integrálem funkce    na intervalu  I. Samotnou funkci pak nazveme integrovatelnou na intervalu  I.

Pro trojné integrály na intervalu    používáme obvykle označení  [3]  nebo  .

Věta (Fubiniova)

Nechť je funkce    integrovatelná na intervalu  .  Pak platí

.

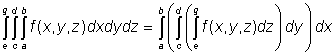Poznámka

Podle Fubiniovy věty můžeme tedy trojný integrál na trojrozměrném intervalu počítat jako trojici integrálů jednoduchých, přičemž podobně jako u integrálů dvojných nezáleží na pořadí integrace. Musíme ovšem zaručit, že hledaný trojný integrál existuje, což je možné například pro spojité integrandy.

Integrály na pravé straně rovnosti nazýváme zpravidla trojnásobnými.


[1] Tj. existuje takové nezáporné číslo  K,  že pro každou trojici  [x,y,z] z intervalu  I  platí  .

[2] Viz Apendix A3.

[3] V námi používané konvenci odpovídá vnitřní integrál vnitřnímu diferenciálu a podobně vnější integrál diferenciálu vnějšímu. Je to obdobné jako u integrálů dvojných.